
文章題で「整理」できない(「整理」の仕方を知らない)子
今回は「文章題」への取り組みをテーマとして、解法というよりは、与えられた問題に対する「整理」方法について記していきたいと思います。
前回の記事では、平面図形の取り組みの中で“やみくも”に問題演習量だけを増やし、“出たとこ勝負”になってしまっているお子様が多いように感じていることを記しました。
そこで今回は、まずは一旦文章を「整理」した上で、できるだけ可視化された状態で求めたいものへ向かっていく方法をお伝えしていきたいと思います。
「○○算」は▲▲を使って解くべき?
よく算数・数学講師の間で(保護者の方を含む場面も)、「『~算』は~を使って解くべき」といった議論がかわされることがあります。
また、判断をしにくい問題における「整理」の仕方が大切なので、処理をするための技を身につけてもらうわけではありません。何せ着眼点(ポイント)を変えれば解き方の見た目も変わりますよね。ここでのテーマはあくまでも「整理」して、問題の判断や未知のものへ向かっていく(できるだけ最短で)こととします。
「線分図」を活用して文章問題を解く
まずは「整理」するといったことの中で、低学年の際にも利用していたことを思い出してみましょう。以前の記事の中でも以下のような計算において「線分図」を利用することについてお伝えしました。

どう求めるのか、求めるものにどう近づいていくのかを理解する上での「整理」方法のスタートのようなものですね。
「和差算」「相当算」で線分図を活用する
線分図は“大きさ” をとらえる上でも可視化できる便利な道具です。以下のような「和差算」「相当算」とよばれる文章題においても“違い(差)”“全体”といったものを認識しやすいですね。
$\rm{A}$組の人数と$\rm{B}$組の人数と$\rm{C}$組の人数を合わせると$100$人です。$\rm{A}$組の人数は$\rm{B}$の人数より$3$人多く、$\rm{B}$組の人数は$\rm{C}$組の人数より$2$人多いです。それぞれ何人いますか。
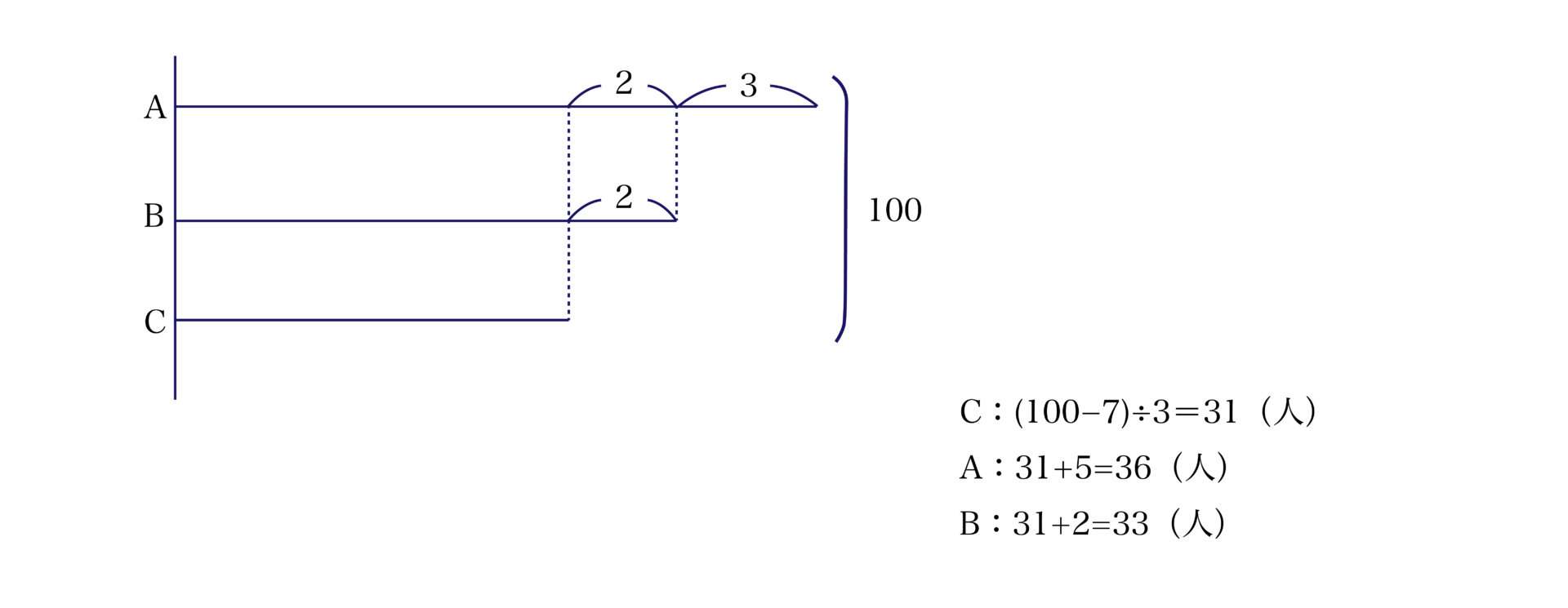
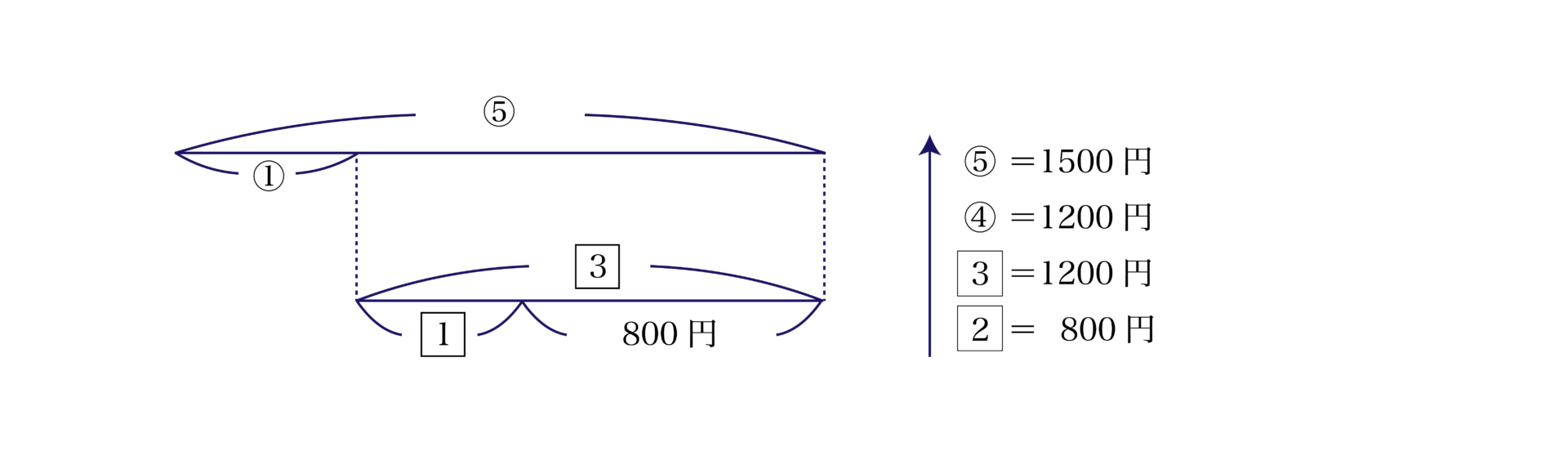
$\rm{A}$さんは$1$日目に所持金の$\dfrac{1}{5}$を使い、$2$日目にその残りの$\dfrac{1}{3}$を使ったところ、残金が$800$円となりました。$\rm{A}$さんははじめいくら持っていましたか。
「流水算」で線分図を活用する
こういった「線」の長さで関係を認識するという意味では以下のような「速さ」の単元においても利用できます。
まずは「流水算」とよばれる速さの単元において、“上り・下り・静水時・流れ”の速さの関係を「線分図」で理解してみましょう。
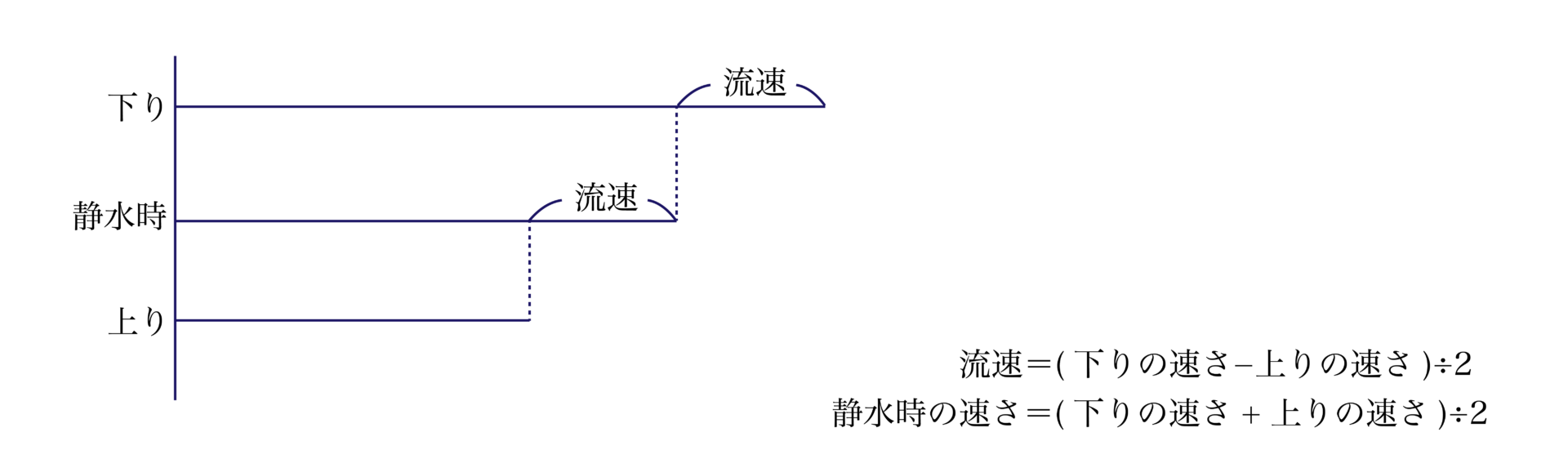
“違い”を明確に可視化できることにともなって、それぞれの関係を認識しやすいですね。
「旅人算」「通過算」で線分図を活用する
さらに「速さ」の単元において、進んだ距離の“和”や“差”を正確にとらえることができます。
以下のような「旅人算」や「通過算」とよばれる速さの単元でも関係の理解のために利用してみましょう。
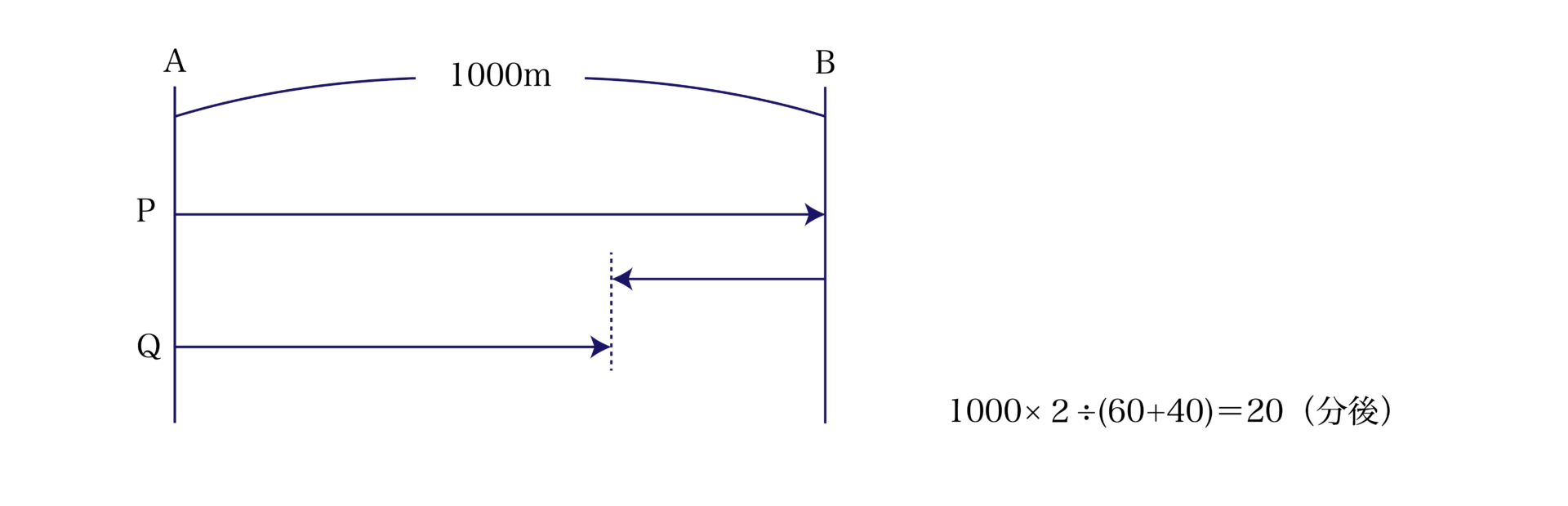
「線分図」を利用することで、$2$人の進んだ距離の“和”が$1000\rm{m}×2=2000(\rm{m})$ということが正確に認識できますね。
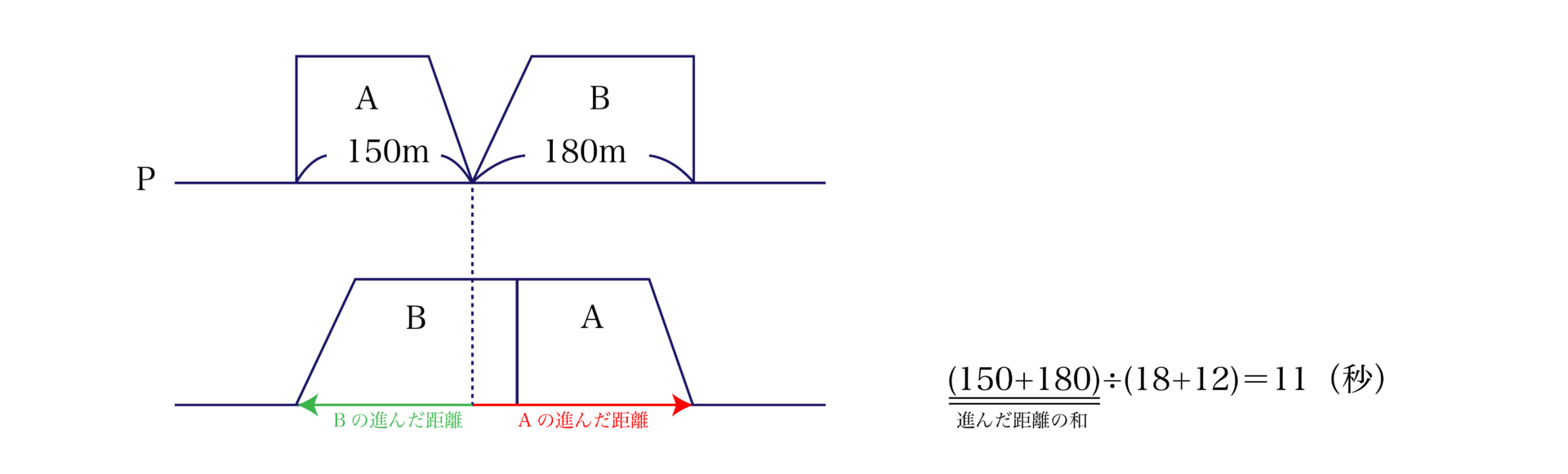
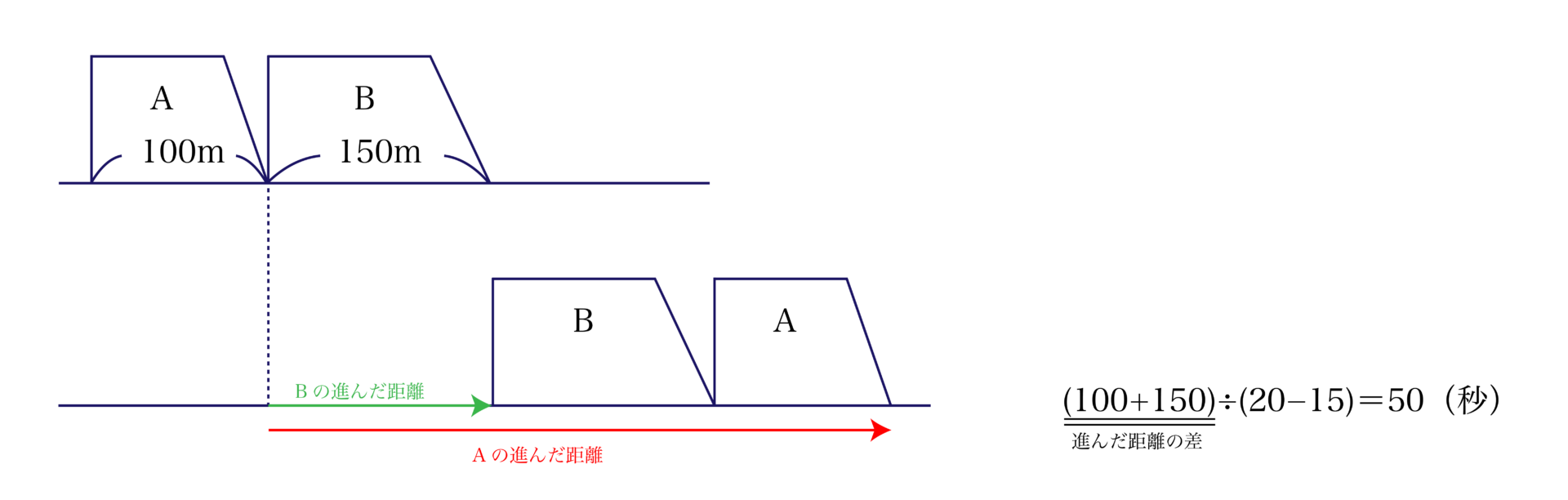
こちらも進んだ距離の“和”や“差”が認識しやすくなりますね。
「線分図」はポイントを明確にするために「整理する」道具の一つ
あくまでも「整理」するための一つの方法です。
自分自身が認識しやすくなる道具を利用してほしいと思います。






















