前回の記事でも“やみくも”に問題演習量だけを増やし、“出たとこ勝負”になってしまっているお子様が多いように感じていることを記しました。いきなり式を立てはじめ、その式の羅列が何を求めるためのものかが理解されておらず、どこに向かっているのかが不明確になってしまっているのですね。まずは一旦じっくりと「整理」することを心がけてほしいと思っています。
文章題の整理方法その2――「表」にする
その「整理」方法の第２回として、今回は「表」を取り上げてみたいと思います。前回に引き続き、ここでもテーマはあくまでも「整理」して、問題の判断や未知のものへ向かっていく（できるだけ最短で）こととします。判断しにくい問題における「整理」の仕方が大切なので、処理をするための技を身につけてもらうわけではありません。
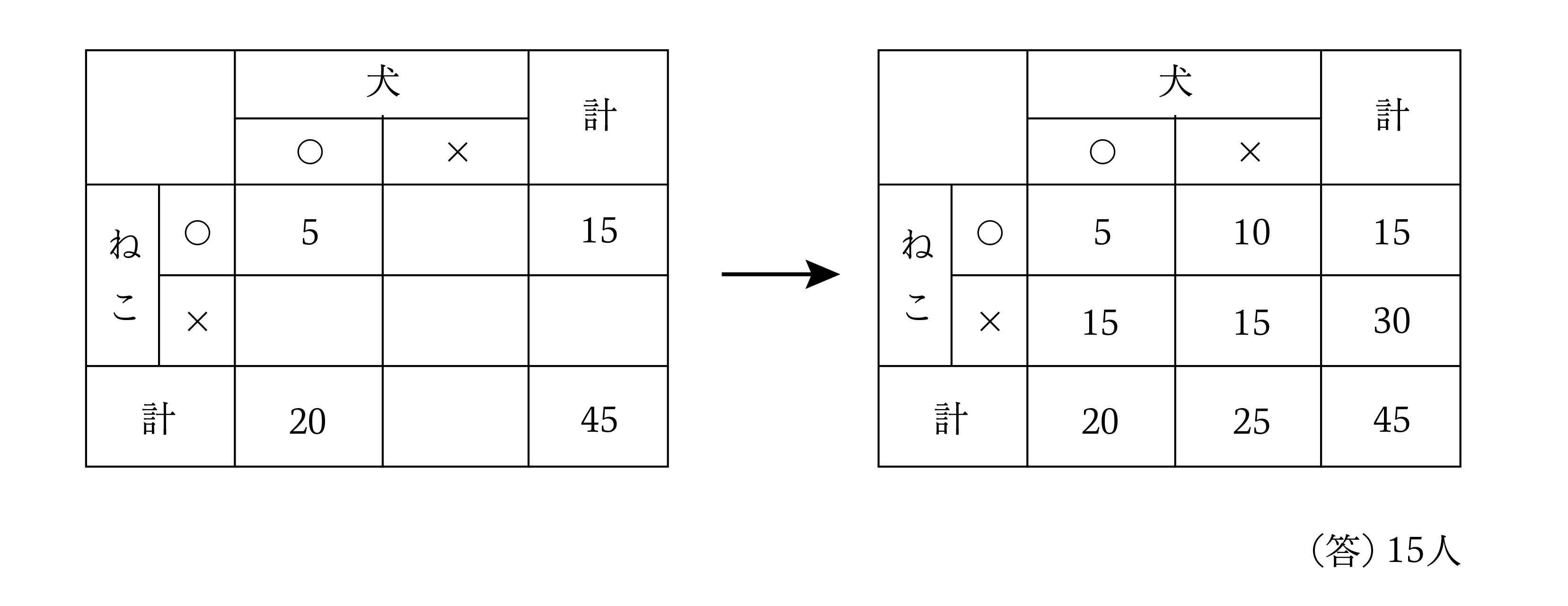
まずは以下のような文章題を「表」に整理してみましょう。
いかがでしょう。
「和差算」「相当算」で線分図を活用する
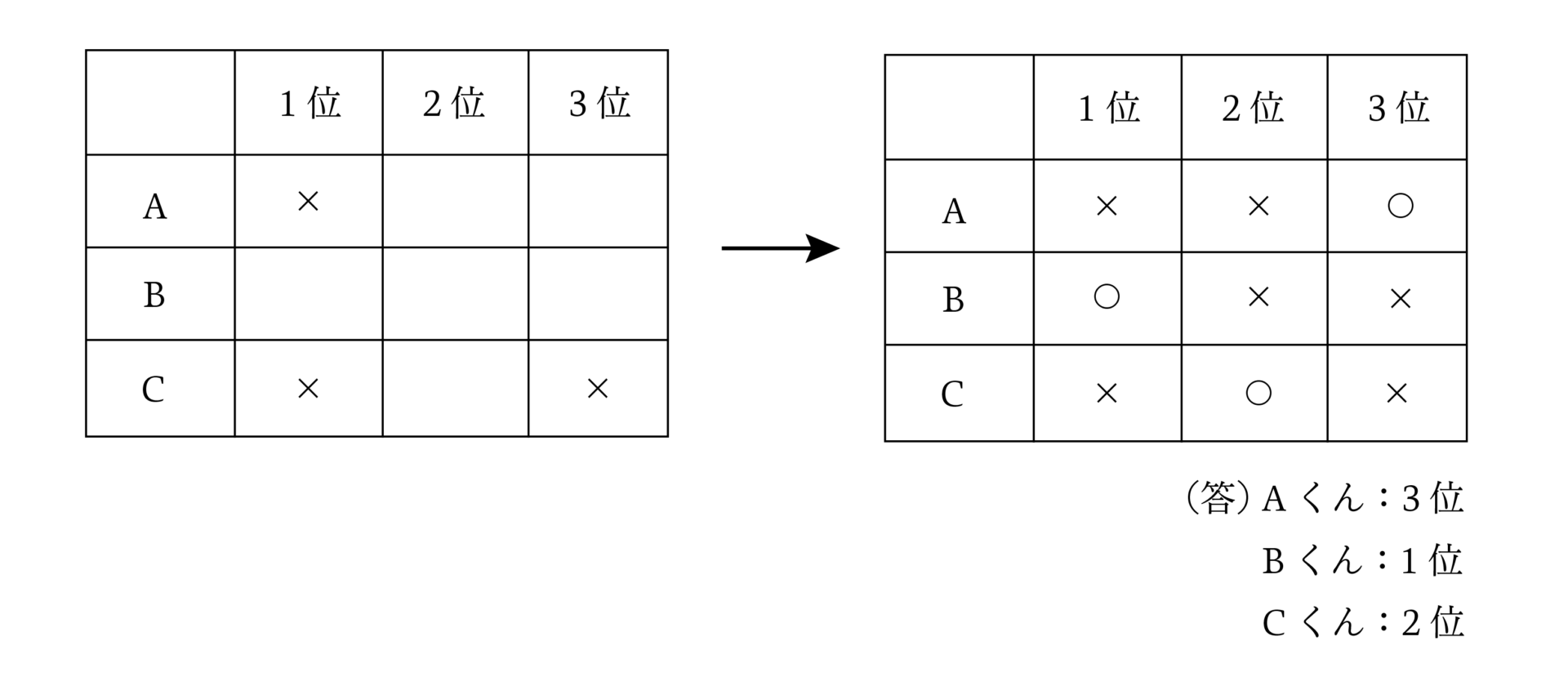
また順位を決める問題等でも「表」に整理することで、コンパクトにまとめられます。
Aくん：「ぼくよりもはやい人がいたよ。」
Bくん：「Cくんは3位ではなかったね。」
Cくん：「でもBくんには負けたよ。」
3人はそれぞれ何位でしたか。
会話から判明する箇所に「×」印を記入していき、最終的には順位が明確になります。以下のような問題でも「表」に整理することで、しっかり分類することができます。
「差集め算」「つるかめ算」で線分図を活用する
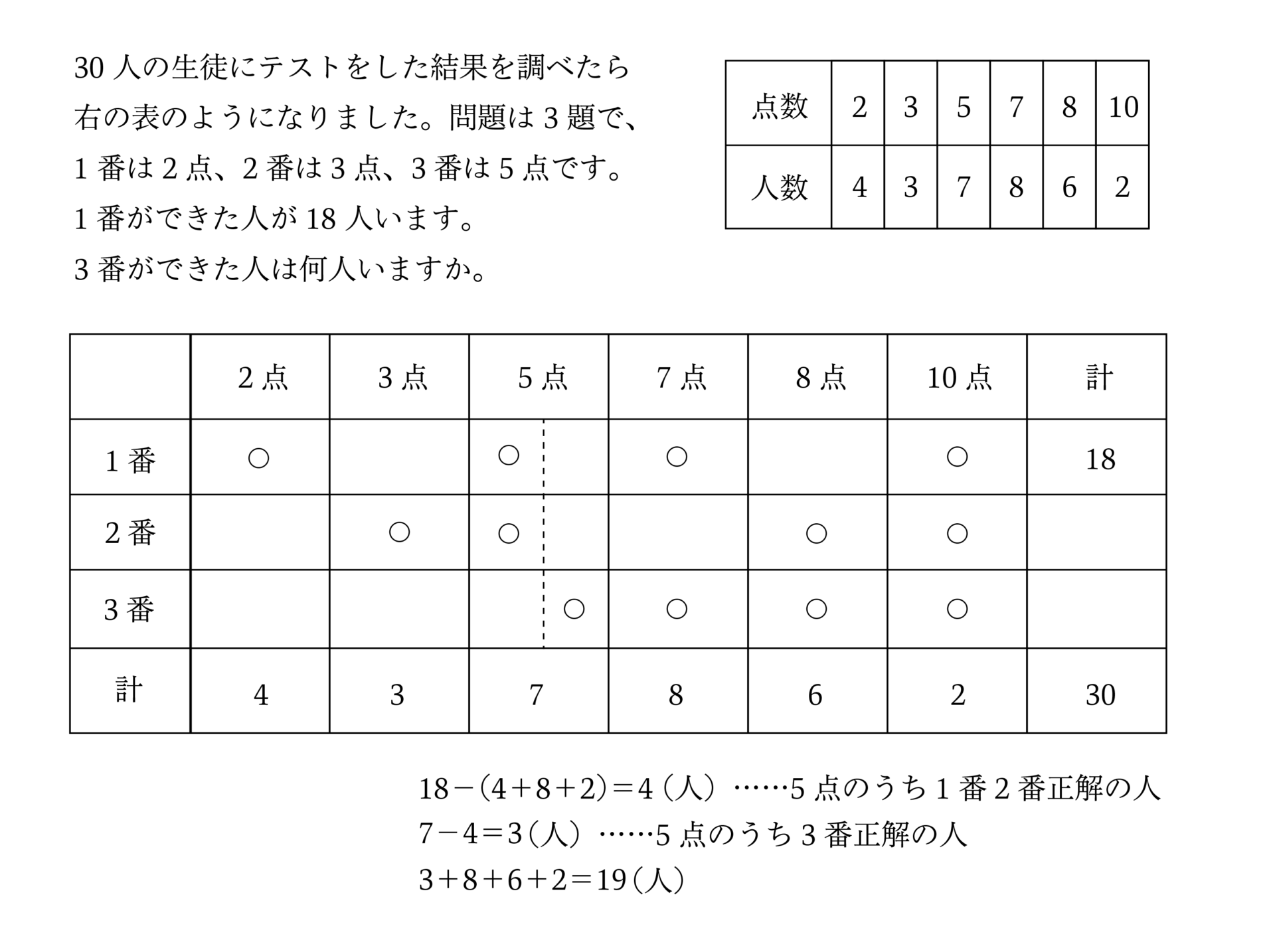
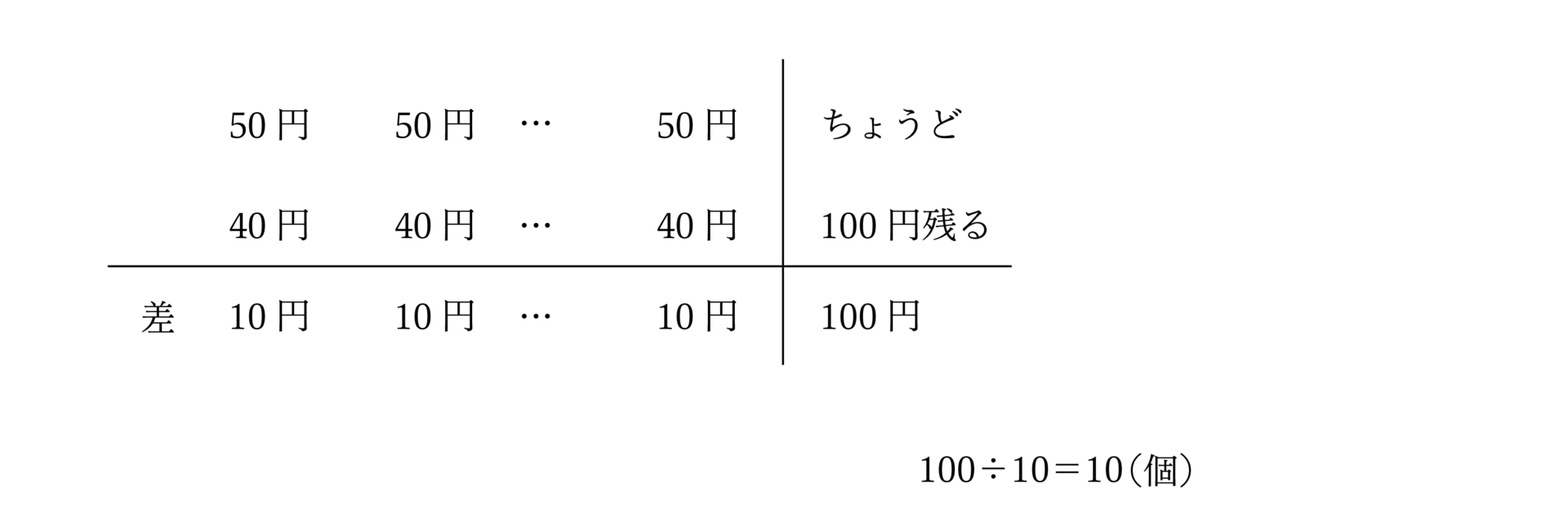
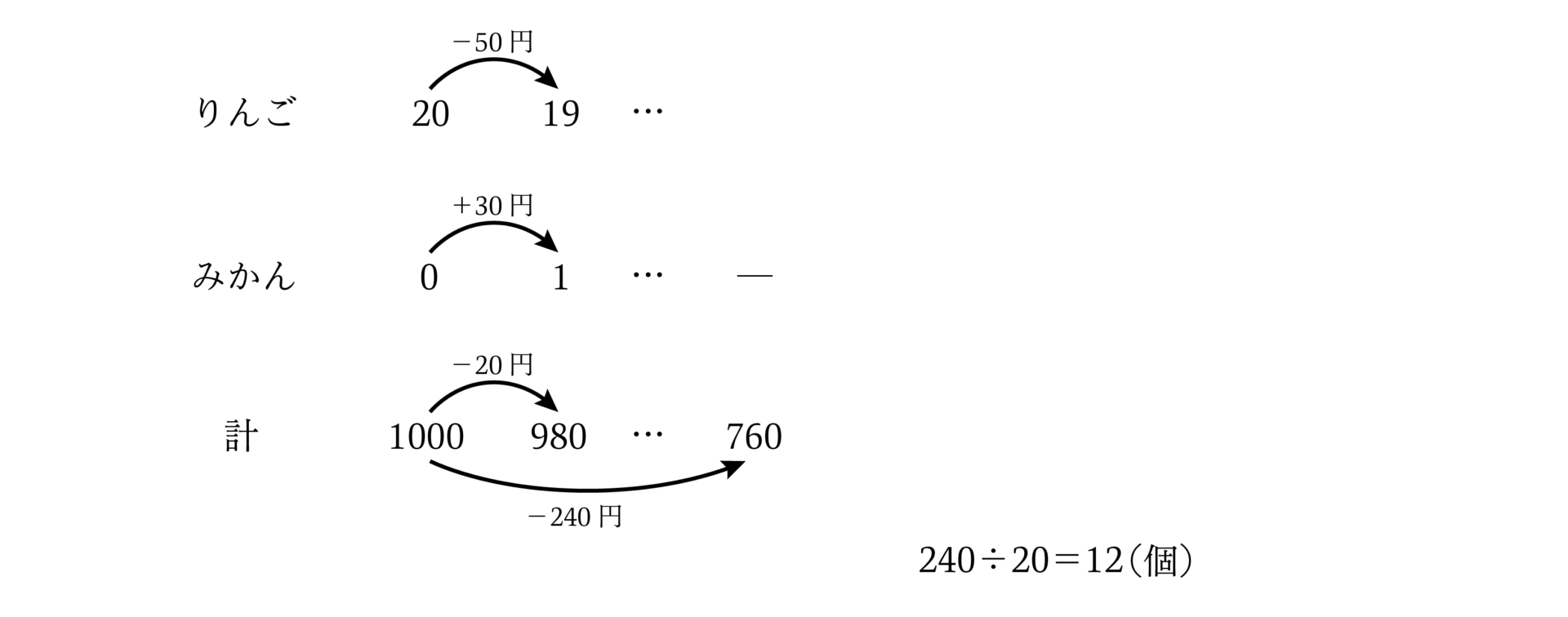
さらに以下のような「差集め算」「つるかめ算」といったような特殊算においても「表」で整理することができます。
1個ずつの差である10円が集まって、全体で100円の差になっていることがよくわかりますね。
はじめにりんごが20個全部あることにすると代金の合計は1000円、そこからりんごを1個減らし、みかんを1個増やすことで20円ずつ代金の合計が減りますね。この「つるかめ算」では以下のような場合でも「表」を活用することができます。
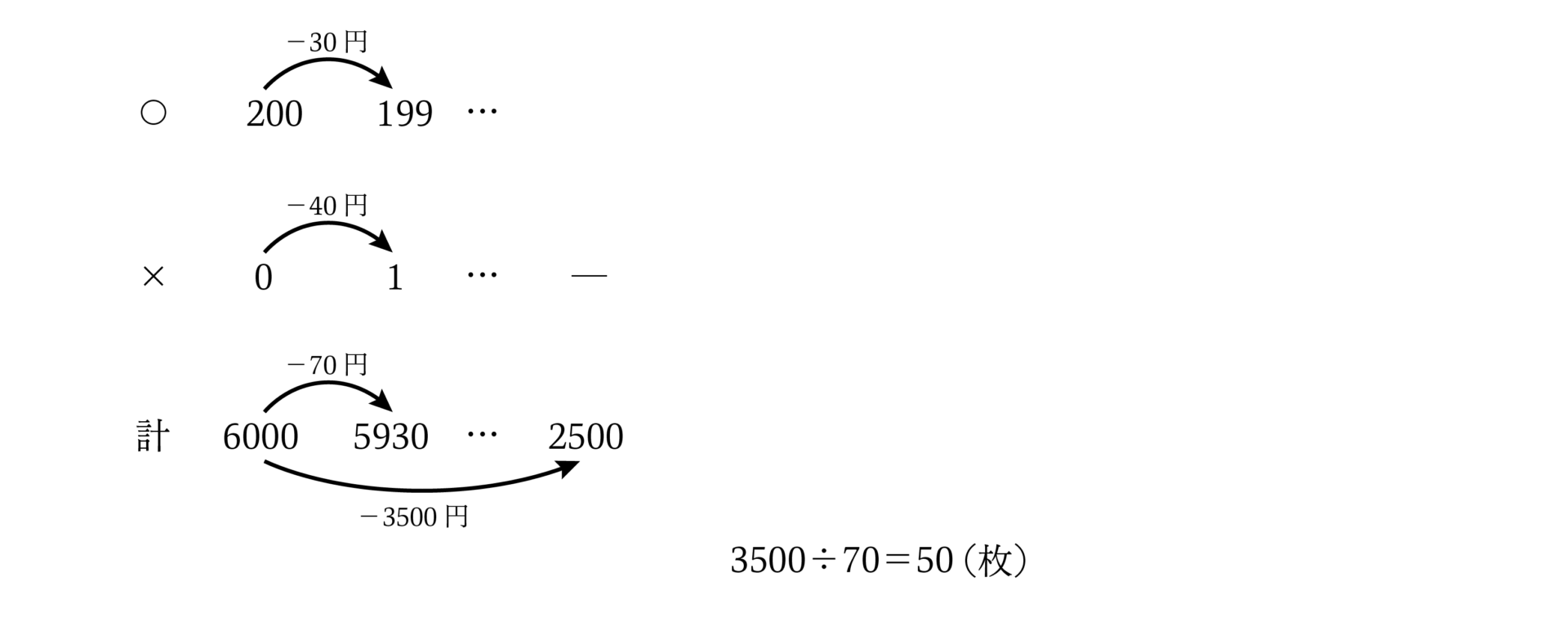
200枚全部運べたとすると賃金の合計は6000円。1枚わってしまうごとに30円もらえないばかりか、40円もべんしょうしなければならないので70円ずつ賃金の合計が減りますね（つるかめ算の中でも「弁償算」とよばれるものです）。
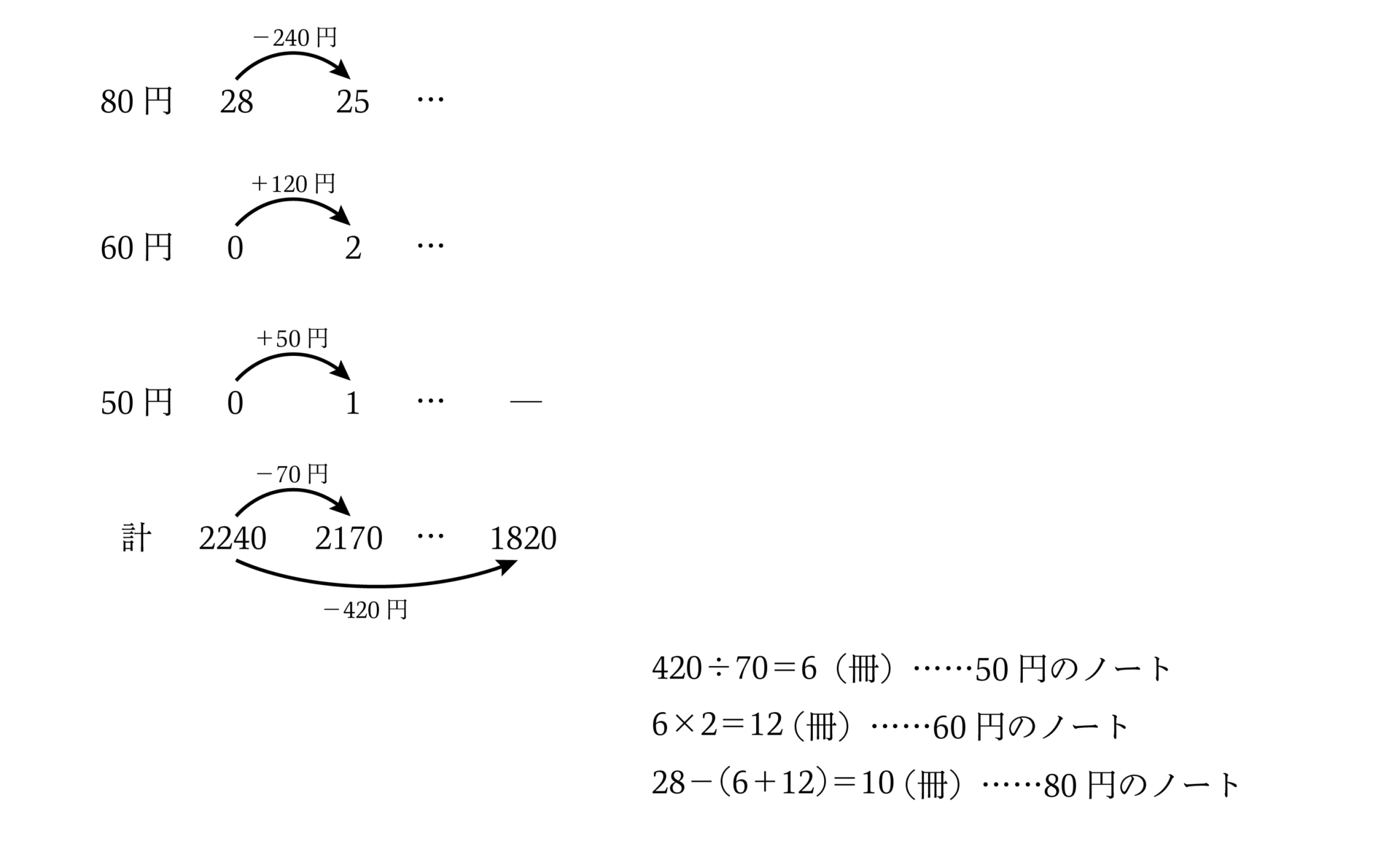
60円のノートの冊数が50円のノートの冊数の2倍になるように調整すると、その分80円のノートは3冊減りますね。このような3種類の場合でも同じような「表」を利用して、同じような処理ができますね。
「和差算」「相当算」で線分図を活用する
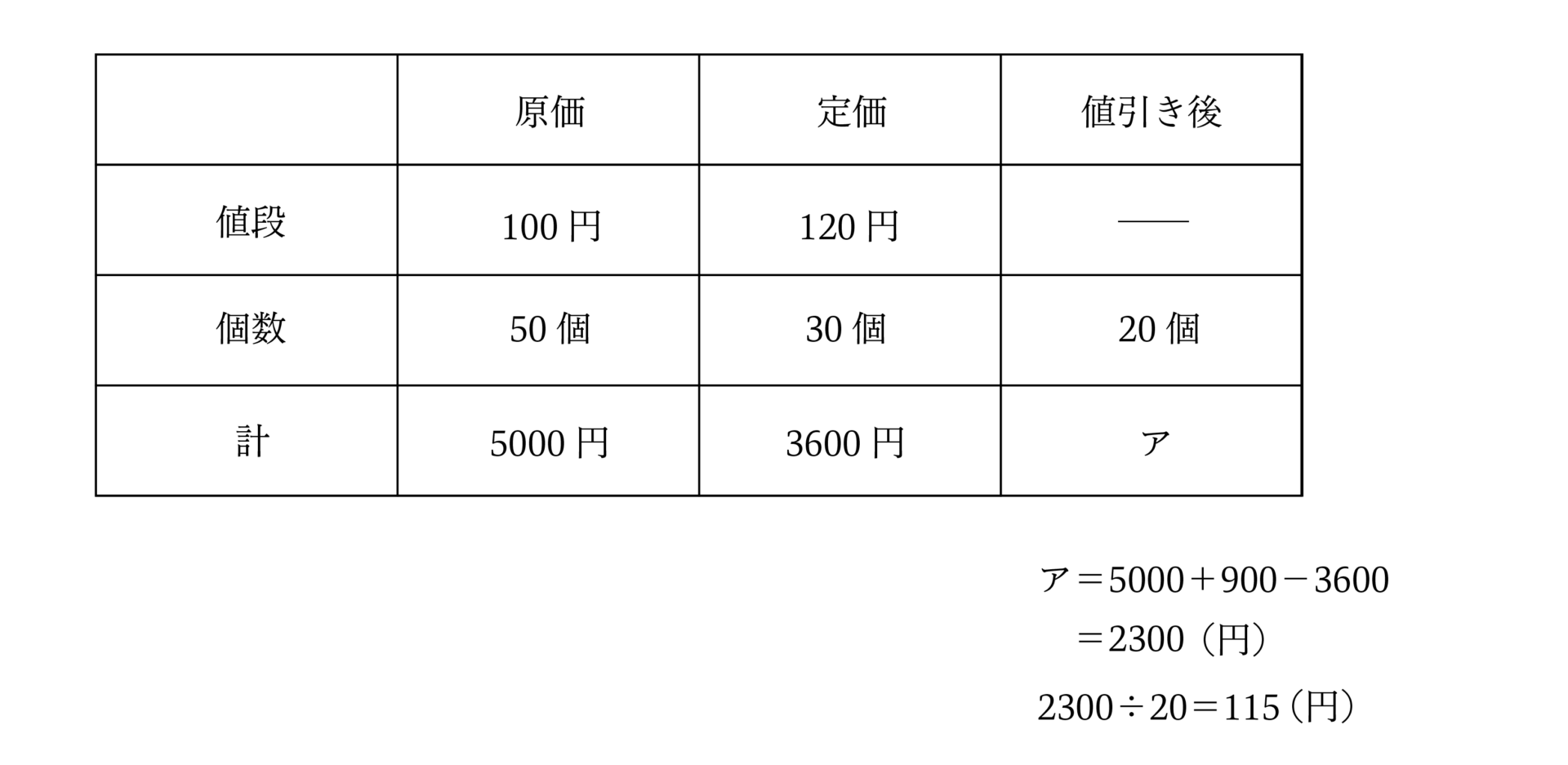
最後にご紹介するのは「商売」の問題です。
「表」にすることで、何を求めれば答えに近づいていけるのかが明確になりますね。
他にもさまざまな場面で活躍する「表による整理」
今回ご紹介した他にも“やりとりの流れ”や“時間の経過”を整理する「表」、場合の数における“調べ”の「表」、規則性における“数値化”した「表」等、様々な場面で利用することができます。
前回の「線分図」ともども問題を整理し、理解を深めるために是非利用してください。
