頭の中の想像には限界あり
前回まで２回にわたって「文章題」をテーマにしてきました。今回は「図形問題」への取り組みとして以前の「平面図形」に引き続き、「立体図形」を扱ってみたいと思います。今まで扱ってきた単元もそうでしたが、それぞれの単元において一から十まで記すことは難しいですし、かつ意味もないことなので、２つのテーマに絞ってお伝えします（“展開図”と“切断”）。その前にここでも過去にあったエピソードから始めます。
不思議な立方体？
小学校３年生の授業において“立方体”を描いてもらう場面がありました。その際には実際のサイコロも見せてあげながら、マス目のノートに描いてもらいました。「先生、描けた！」と多くの子供たちが自信満々に見せてくれました。正しく描けている子もいましたが、思った以上に以下のような“立方体？”を描く子が多いことに驚きました。
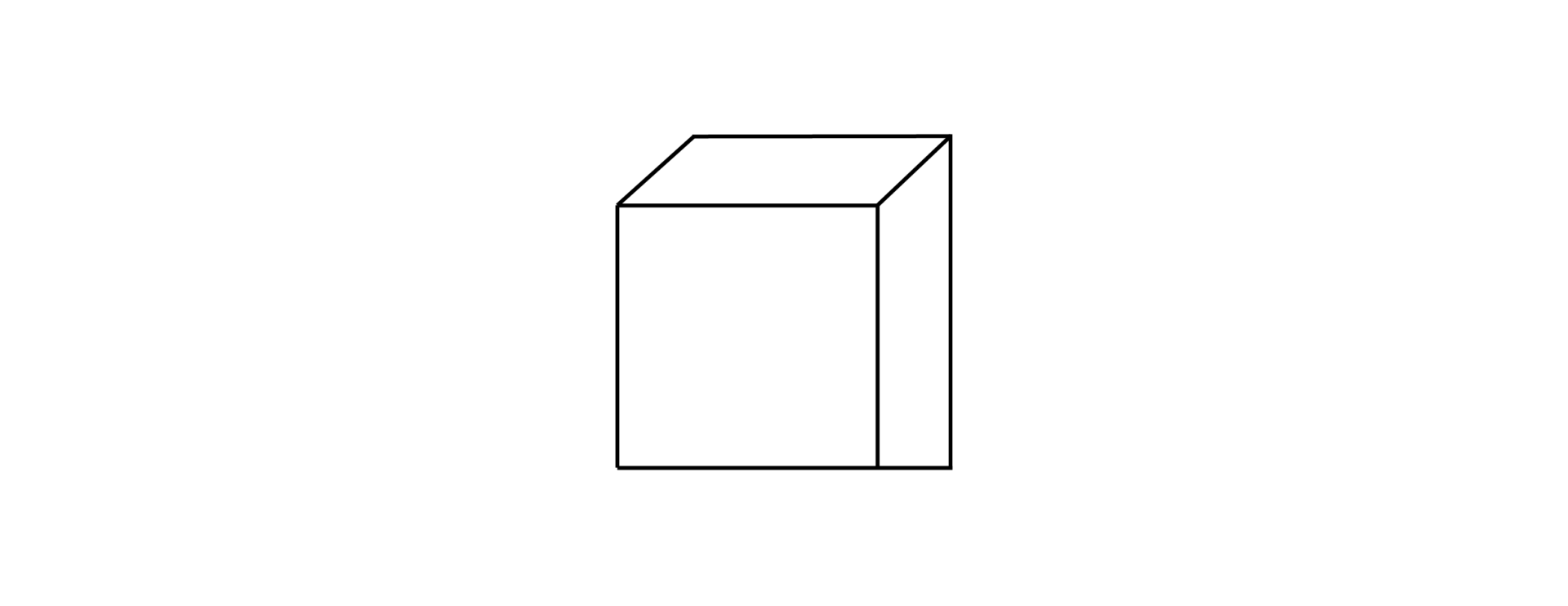
正しく描けているかどうかは、他の単元（計算等）ができるできないとあまり相関関係もなく、上手か下手かもあまり関係がないように感じます。しかも気になったのは、上のような図を描いて“おかしいかな？”と感じていないことです。
算数学習の土台作り
以前の「平面図形」を扱った際にも記しましたが、実際の“モノ”をいろいろな方向から見たことが少ないんだなあとここでも実感します。またその図形の意味（性質）を捉えながら“手を使って”描いてきてないんだなあと感じます。
とはいえ、そもそも３次元のものを２次元の平面上に描いて取り組むものなので、形に対しての理解が進んでもその先が“想像”だけになってしまっては厳しいですよね。そこで、想像だけには頼らずに土台から一歩踏み込んだ部分に対するしっかりとした“手順・方法”を学んで利用してほしいと思います。
「展開図」に関する問題
「立体図形」を題材とした問題も様々な種類があります。その中の一つ「展開図」をまずはテーマとしましょう。
展開図を完成させ「見取り図」を描く問題
「展開図」を組み立てて立体図形が完成し、上記のような「見取り図」を描くということになります。以下見てみましょう。
“手順・方法”なしにやみくもに想像力に頼ると間違いが起こりがちな問題です。しかしながらきちんとした“手順・方法”を利用することで、何となくではない確信をもった解答を出せることになります。
解説
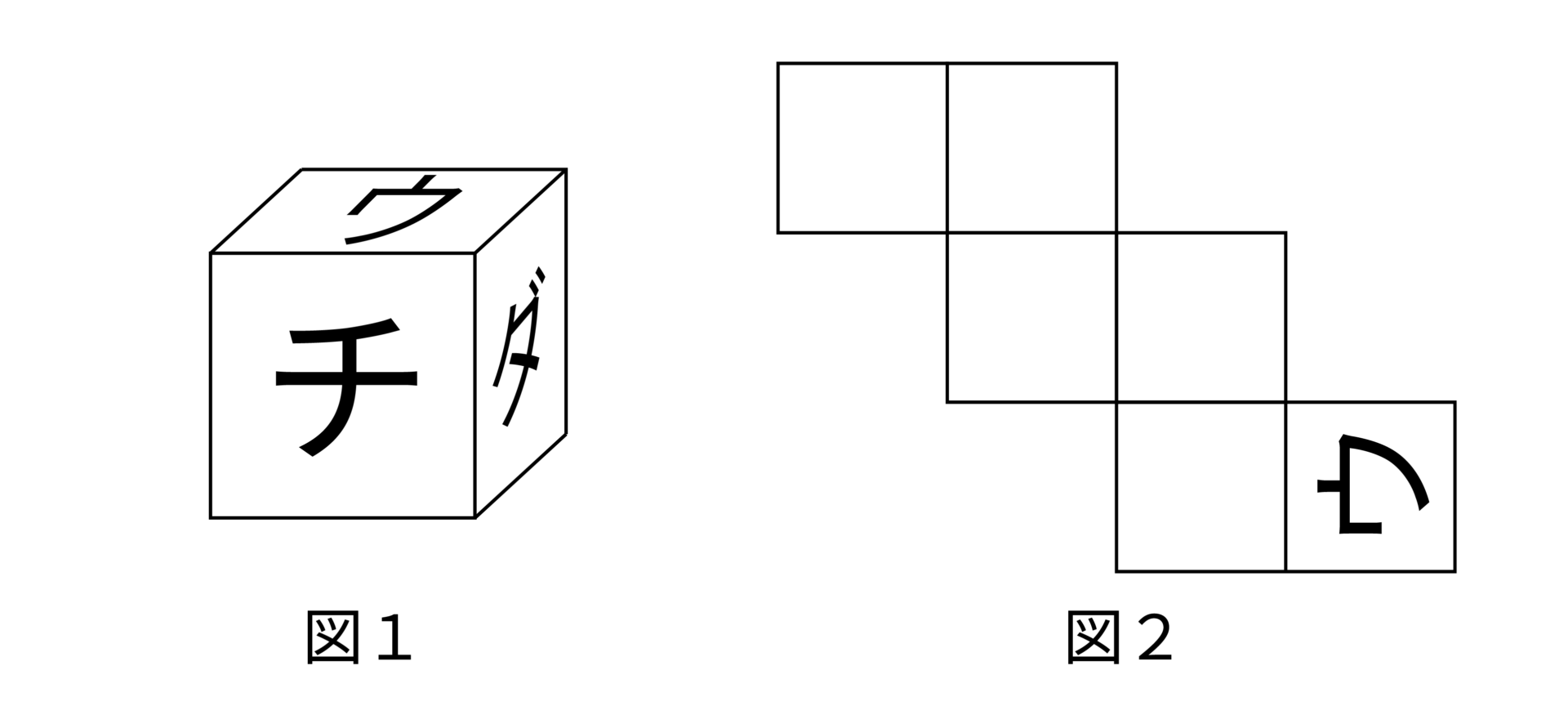
まずは見取り図・展開図それぞれに「頂点記号」をつけてみましょう。その際立方体の対角線上にあたる一番遠い点（図の→の位置関係）は、展開図上では以下のように２つの正方形の面の対角線上にありますね。
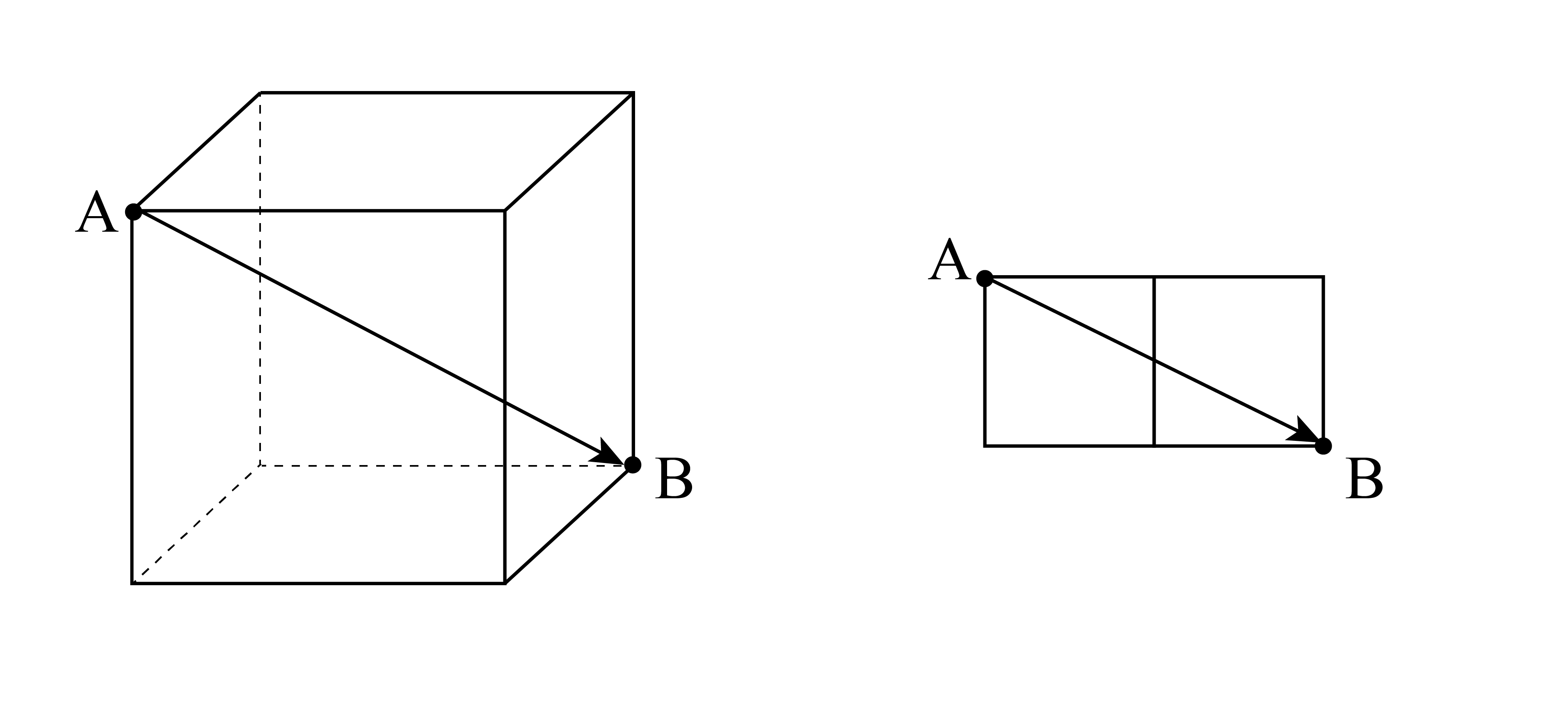これを利用すると、以下のように展開図内の頂点が次々決まります。
そして、「チ」と「ダ」の書いてある面が決定し、頂点をつき合わせることで向きも正しく書くことができますね。
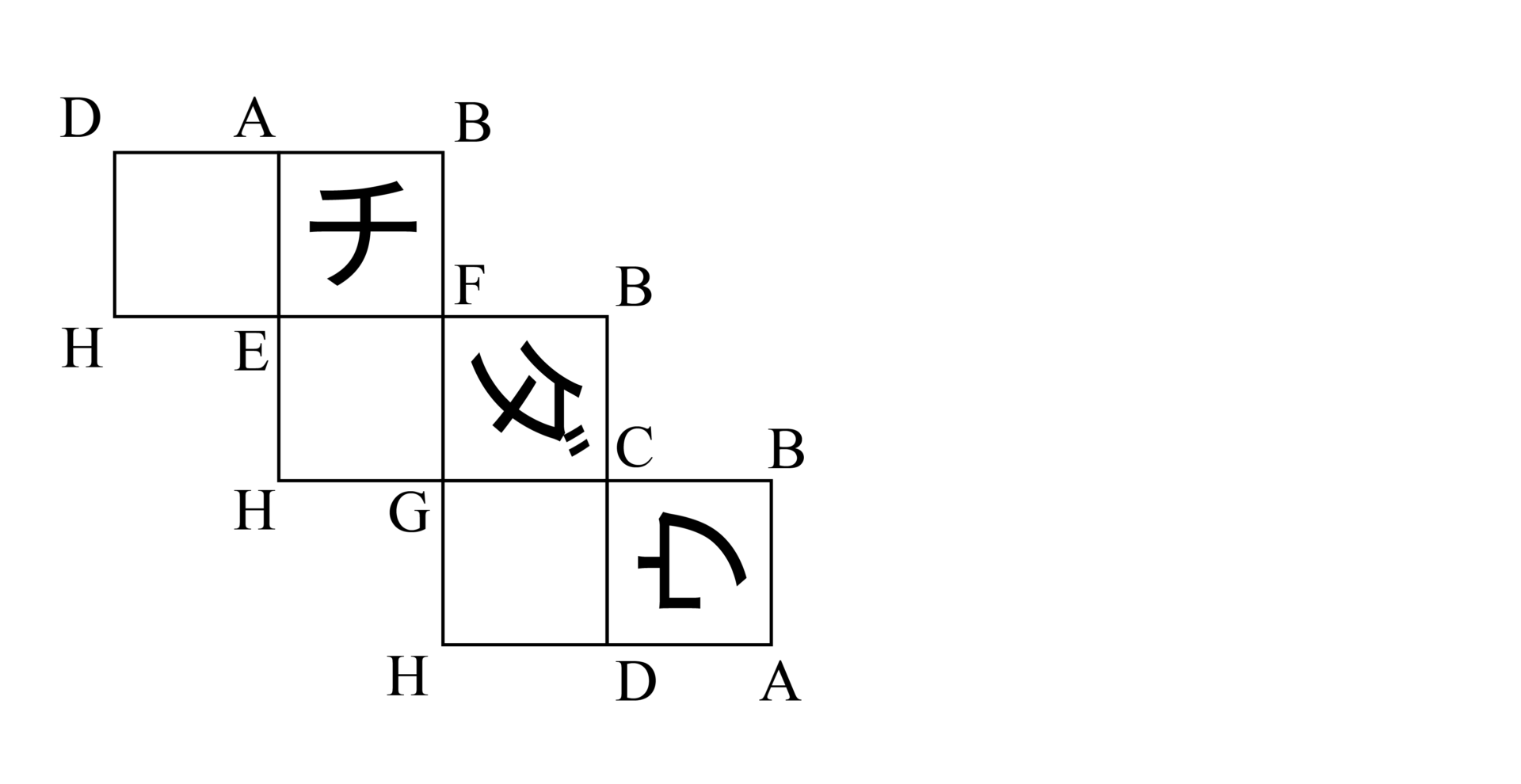いかがでしょう？想像だけに頼ると字の書いてある面は何となく判明しても、向きまで完全に正しくとなると意外にやっかいですよね。そこで利用した手順・方法が「頂点記号打ち」（その際“最も遠い点”の関係を利用）でした。
組み立てた立体の体積を求める問題
次は展開図が与えられていて、組み立てた時の立体の体積を求める問題です。
実はこの問題もかつて小学校５年生や６年生に取り組んでもらったことがあります。多くの子供たちはどんな取り組み方をしていたでしょう？
何はともあれ、まずは見取り図を描かなければということで、
「三角形の面が角（つの）みたいに突き出したぞ！」
「くっつかない辺があるから立体にならないよ～！」
なんて言いながら描いた図を見せてくれました。頑張ってくれたことを評価しつつも、「どうやったらこの立体の体積が出せるの？」といった、ものすごい見取り図のオンパレードでした（今となってはとても子供たちの描いた図を再現することはできません（笑））。
解説
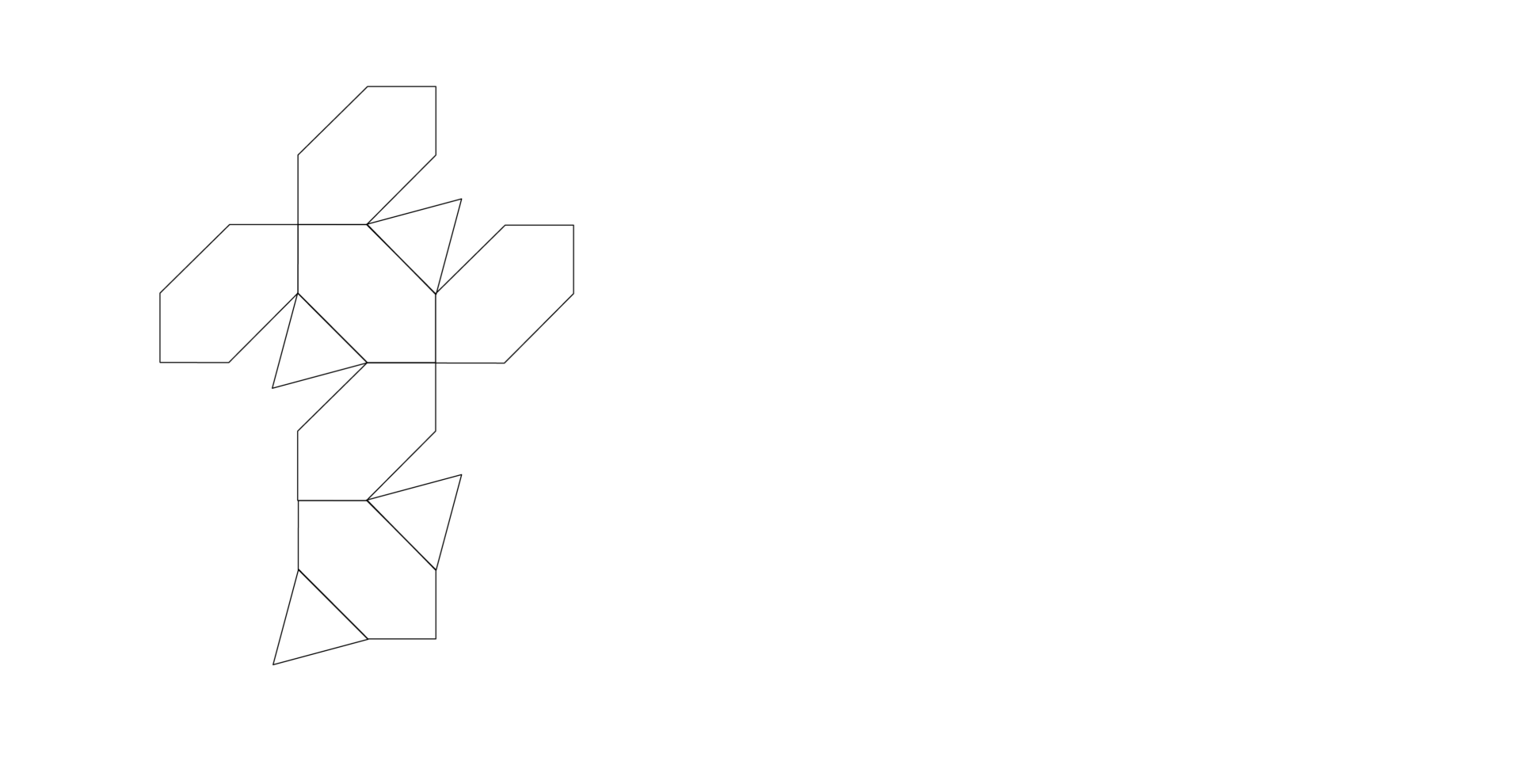
一つ目の問題以上に“手順・方法”なしに想像力だけに頼ってしまうとたいへんなことになりそうです。ここでは展開図を無理やり組み立てるのではなく、もともとは「基本立体」で、その一部分を切り取った形であるという考えを利用しましょう。ここでの基本立体は、六角形の面が６つある情報をもとにして“立方体”にしてみましょう。
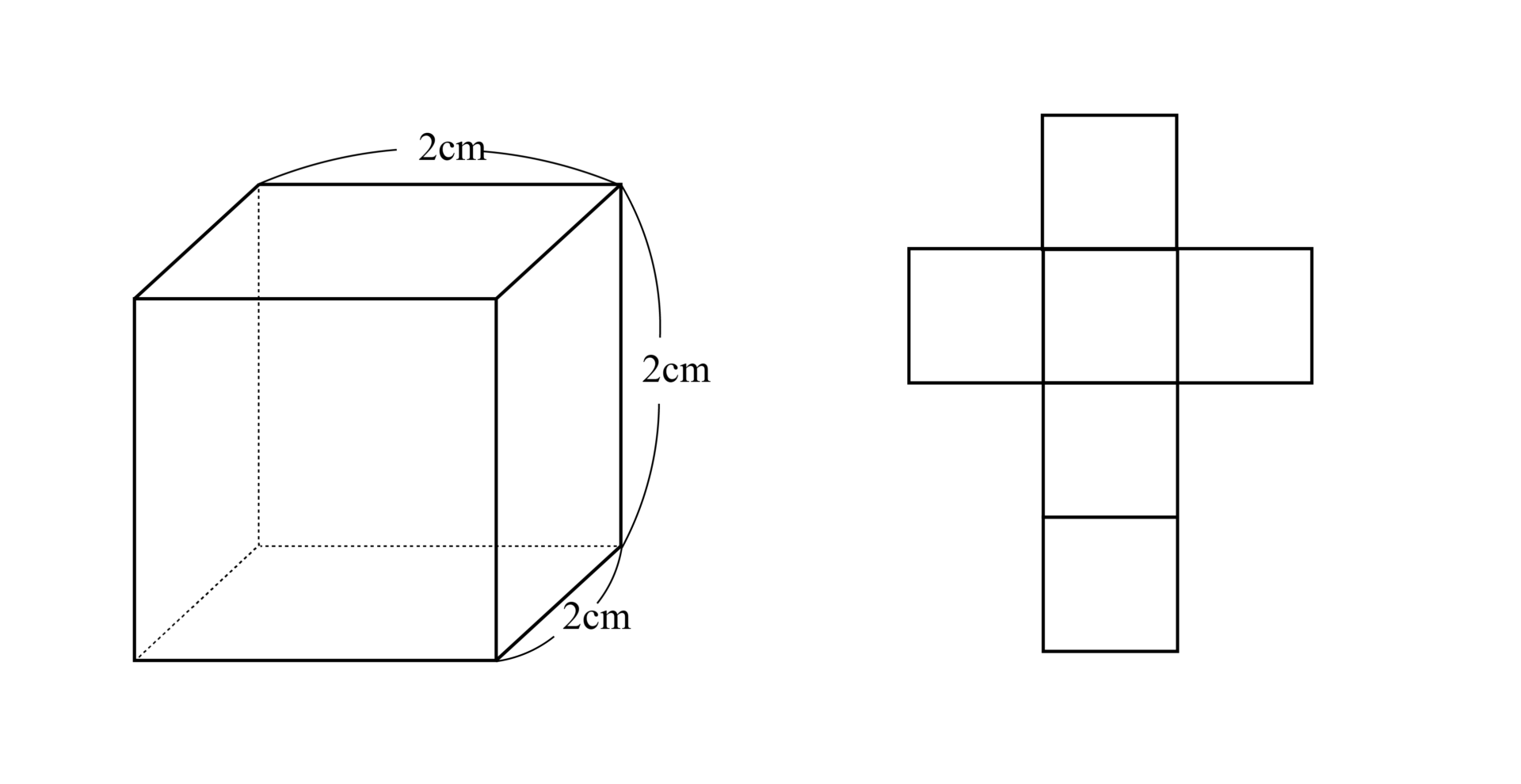１辺が２cmの正方形の面から等しい２辺の長さが１cmの直角二等辺三角形２つを切り取ってみると、
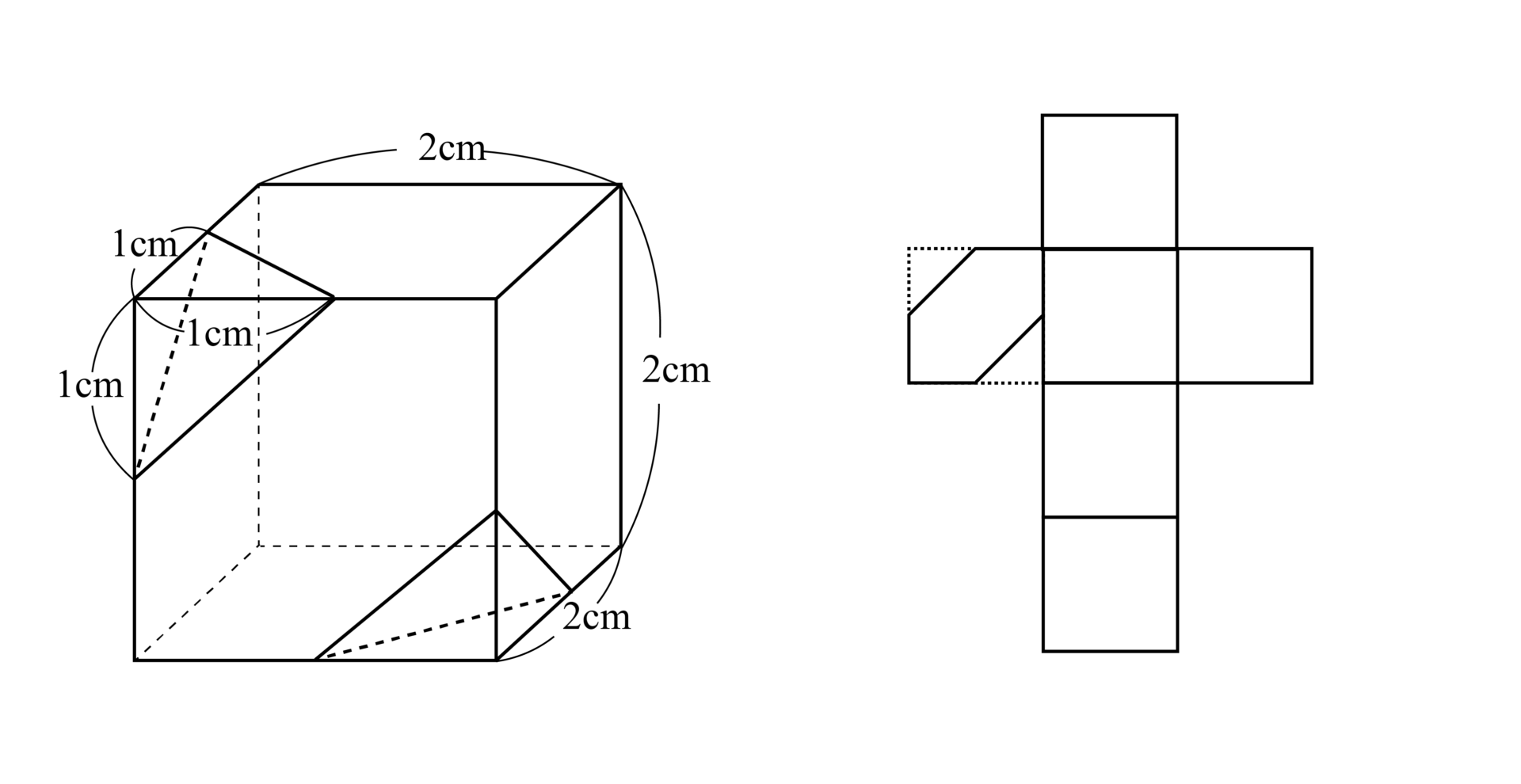
六角形や正三角形の面が作り出されてきました。さらにこれをくり返すと、
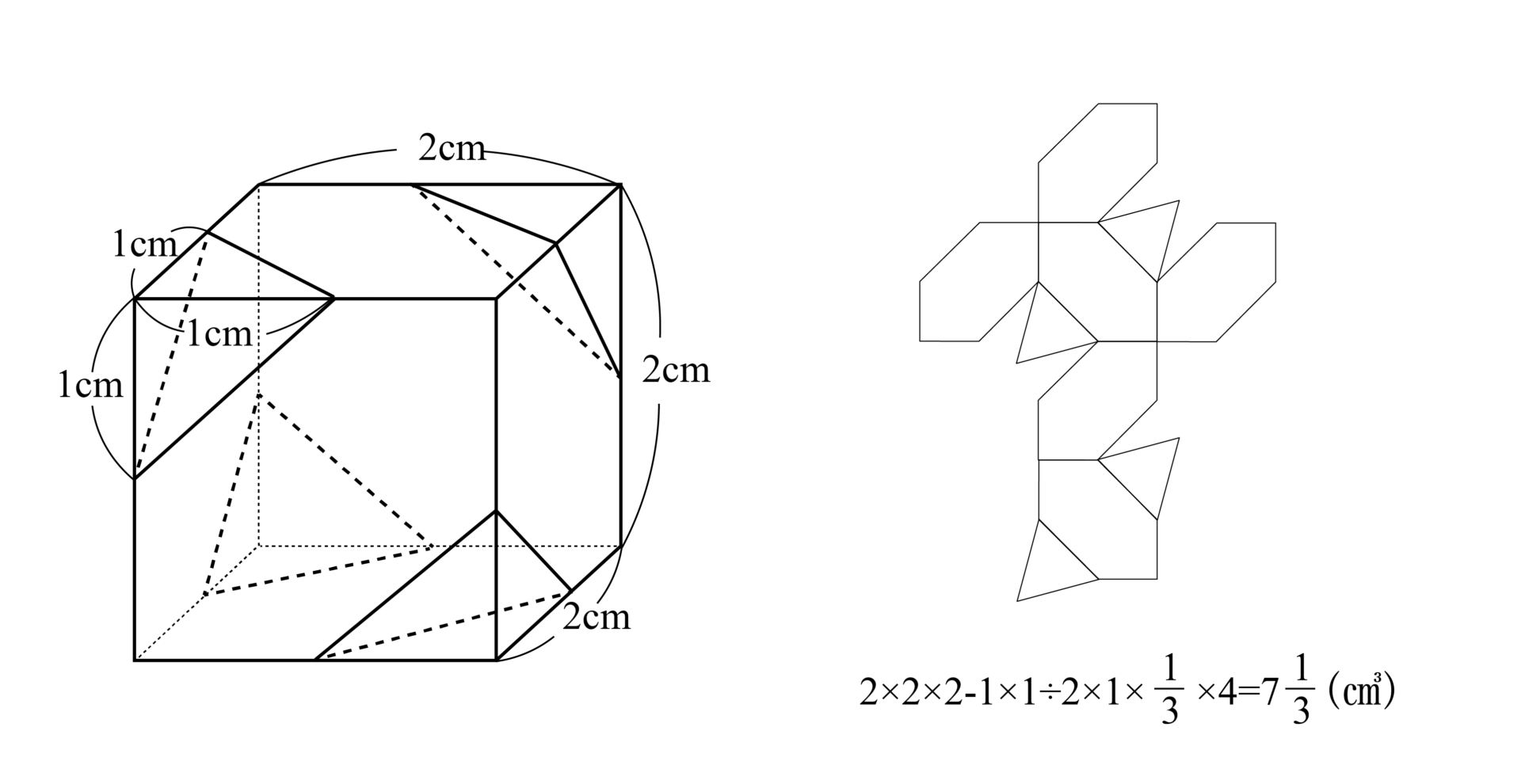ここでも想像だけに頼ることなく、「基本立体からの切断」といった“手順・方法”を利用することで、きちんと体積を求めることができました。
低学年のうちは「空間認識能力」の向上を意図して“実物”を見たり作ったりすることが大切です。その後、平面上に描きながらどんな形なのかの“理解”をした上で、“手順・方法”を手に入れて利用していってほしいと思います。
次回は「切断」における“手順・方法”をお伝えする予定です。お楽しみに。
