前回まで立体図形を扱ってきましたが、今回からは「数の性質」について記していきたいと思います。
入試においてももちろんですが、算数・数学の学習の中でも大変“差”のつく単元でもあり、“興味・関心”“知識量”といった面でも個人差を感じます。そういった点からしても、他の単元以上に絞って扱わないといくら誌面があっても足りません。
今回の「数の性質」においても2つくらいのテーマに絞ってお伝えします。
その1「素因数分解」の利用
まずはその数の分野の中でも大元となる“素数”について見てみましょう。
素数とは“$2$以上の自然数で、(正の)約数が$1$とその数自身のみであるもの”です。
別の言い方をすれば、“(正の)約数の個数が$2$である自然数”のことです。
小さなものから並べると、$$2, 3, 5, 7, 11, 13, 17, 19, 23, 29, ……$$で、$100$以下の素数は$25$個あります(ちなみに$1000$以下の素数は$168$個あります)。
合成数を素数の積の形で表す「素因数分解」
この素数が元となって、それ以外の自然数(合成数)は素数の積で表すことができます。
この素数の積の形で表すことを「素因数分解」とよびます。
例えば、
$24$は $2 \times 2 \times 2 \times 3$
$2023$は $7 \times 17 \times17$ と表すことができます。
例題で素因数分解の活用法を確認する
それでは今回はこの「素因数分解」を利用した問題に焦点を当てて見ていきましょう。
割り切れ回数
もちろん、直接$120$を$2$で割り続けても答えは出せますが、$120$を素因数分解してみると、$$120=2 \times 2 \times 2 \times 3 \times 5$$
となり、明らかに$2$で$3$回割り切れることがわかりますね。
(答え $3$回)
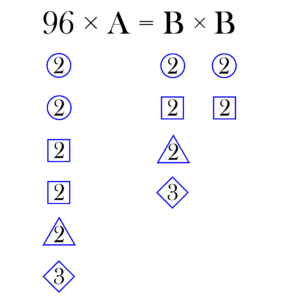
平方完成
$96$を素因数分解してみると、
$96=2 \times 2 \times 2 \times 2 \times 2 \times 3$
これを以下のように振り分けてみます。
すると、△$2$と◇$3$のペアが一つずつ不足していますね。
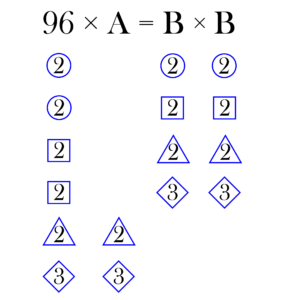
そこで以下のように補ってみると、
$\rm{B} \times \rm{B}$(平方数)が完成しますね。
(答え $\rm{A}=6, \rm{B}=24$)
既約分数の個数
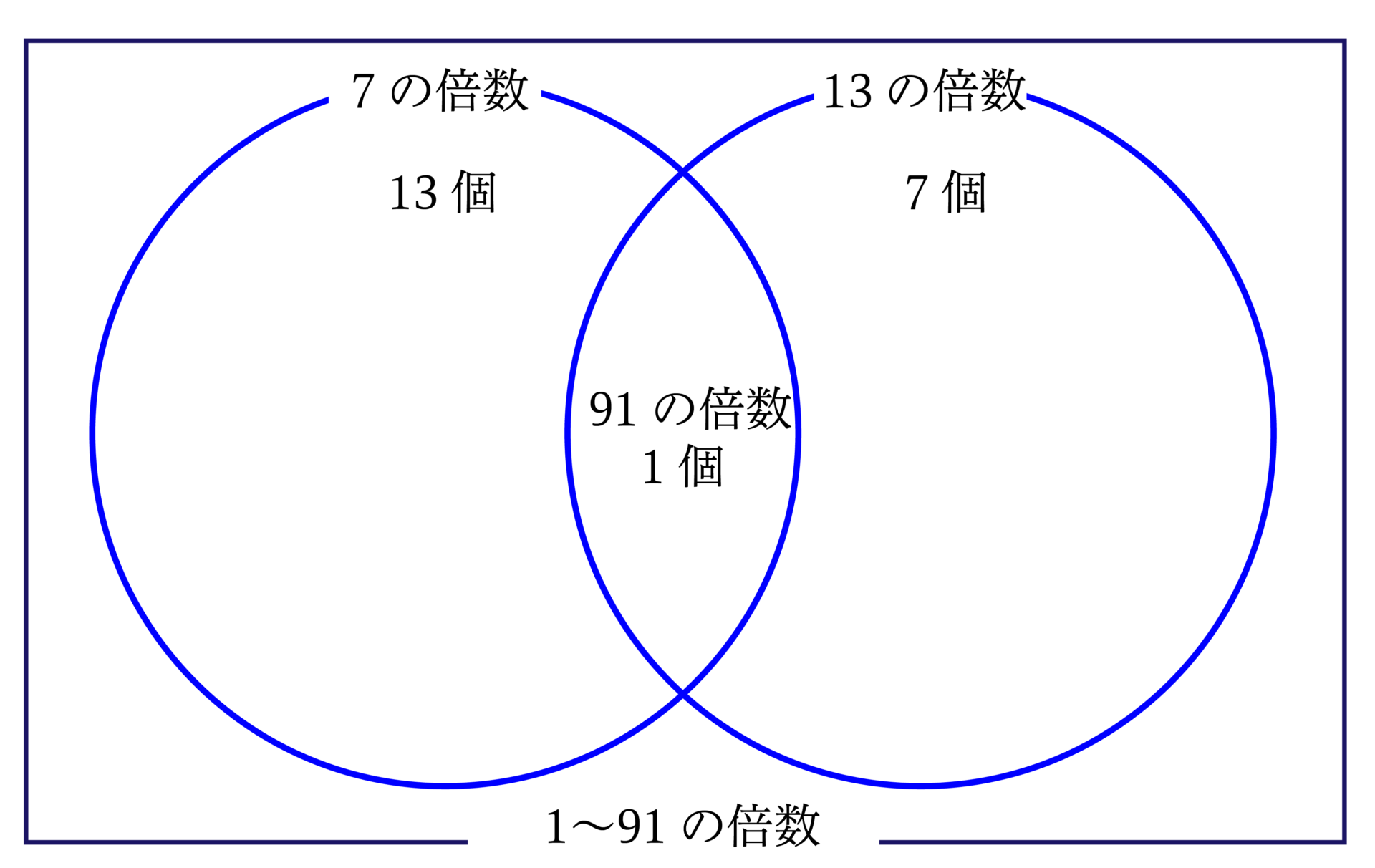
分母の$91$を素因数分解してみると、$$91=7 \times 13$$なので、分子に$7$の倍数や$13$の倍数があると、その分数は約分できてしまいますね。
分子の$1$から$91$までの$7$の倍数や$13$の倍数の個数は、以下の“ベン図”を利用するとイメージしやすいでしょう。
$13$個$+7$個$-1$個$=19$(個)
よって、約分できない分数(既約分数)は、
$91$個$-19$個$=72$(個)
(答え $72$個)
約数の個数・総和
これについてももちろん書き出してもよいのですが、問1~3と同様に素因数分解を利用してみましょう。
$$72=2 \times 2 \times 2 \times 3 \times 3$$
分解された一つずつ(素因数)を組み合わせたものが約数となりますね。これを以下のような表でイメージしてみましょう。
| $1$ | $2$ | $2 \times 2$ | $2 \times 2 \times2$ | |
| $1$ | $1$ | $2$ | $4$ | $8$ |
| $3$ | $3$ | $6$ | $12$ | $24$ |
| $3 \times 3$ | $9$ | $18$ | $36$ | $72$ |
個数はこの表の中にあらわれる$12$個となりますね。
ちなみにこの個数は素因数分解の式
$72=2 \times 2 \times 2 \times 3 \times 3$
を、$2^3 \times 3^2$と表すと、右肩に出てくる数(指数とよばれますね)に$1$加えたものの積
$(3+1) \times (2+1)=12$(個)
となっていますね。
これを利用して約数の総和も求めてみましょう。
あらわれた$12$個の約数$(1,2,4,8,3,6,12,24,9,18,36,72)$の和は、$$(1+2+2^2 +2^3 ) \times (1+3+3^2 )=195$$
となります。
今回は「数の性質」の中でも大変利用頻度の多い“素因数分解”をテーマとして記してみました。上記の問題例以外でも様々な場面で利用することでしょう。
次回は「数の性質②」として“余り”に注目した問題をテーマとしたいと思います。