
「数の性質」において、前回は“素因数分解の利用”をテーマに扱いました。
今回はその「数の性質」第2弾として“剰余(余り)”に注目してみたいと思います。
ますます中学入試においても取り上げられていくことでしょう。
それでは以下“余り”に関する問題を見ていきましょう。
「あまりが同じ」
3で割ると余りが2、5で割っても余りが2となる整数のうち、小さい方から5番目の整数を求めなさい。
3で割ると2余る数(3の倍数+2)、5で割ると2余る数(5の倍数+2)のイメージを“線分図”であらわすと、
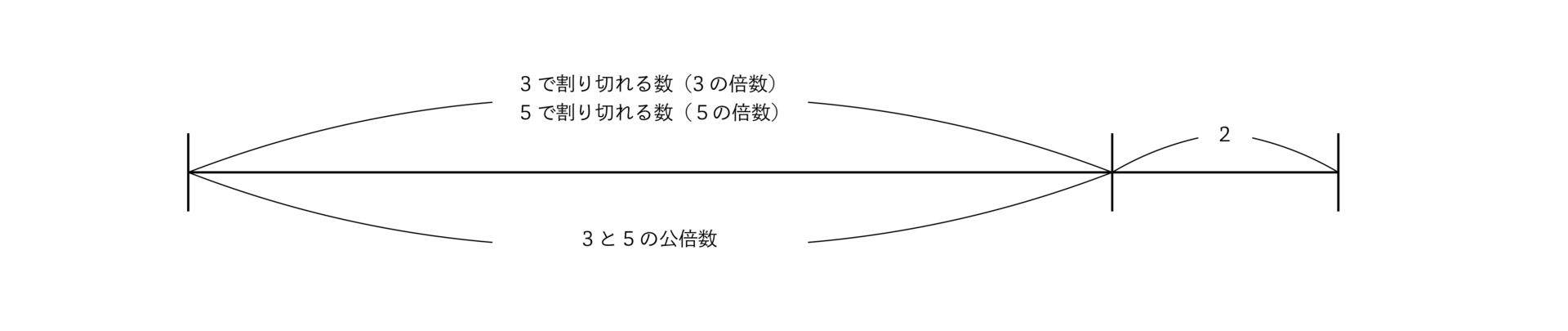
となりますね。
3と5の最小公倍数は15ですから最も小さい数は15×0+2=2
5番目は、15×4+2=62_となります。
「不足が同じ」
8で割ると6余り、11で割ると9余る整数のうち、小さい方から5番目の整数を求めなさい。
8で割ると6余る数、11で割ると9余る数のイメージを“線分図”であらわすと、
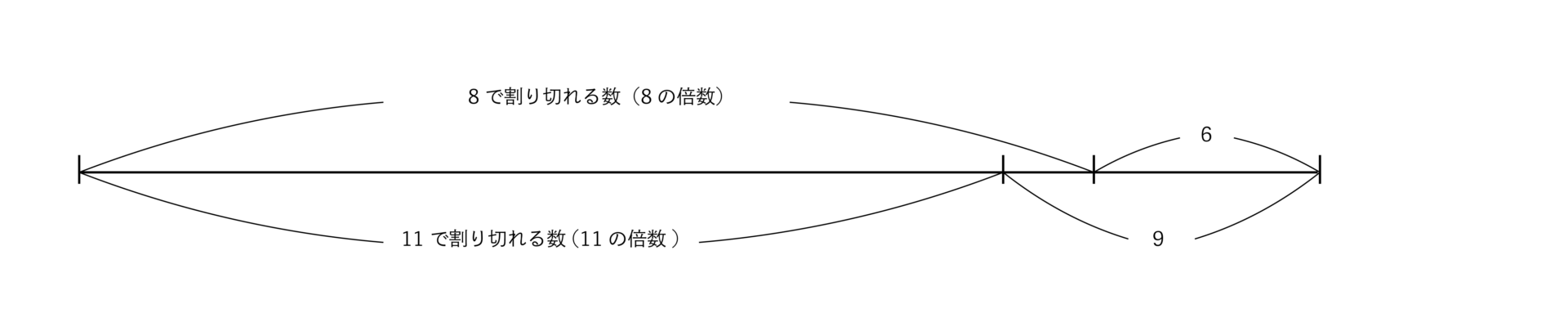
となりますね。
【問1】と違い8の倍数の長さと11の倍数の長さが一致しません。そこで、
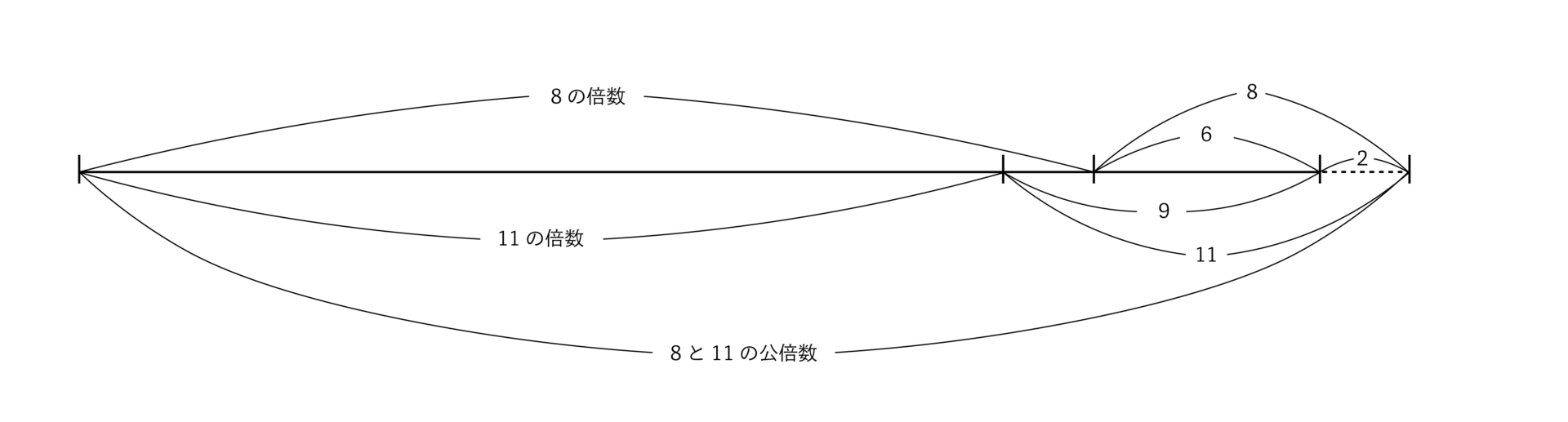
というようにあと2伸ばしてみると、8の倍数に8加えた長さは8の倍数、11の倍数に11を加えた長さは11の倍数となりますね。8と11の最小公倍数は88ですから、最も小さい数は88に2足りない(不足する)数である88×1−2=86
5番目は
88×5−2=438となります。
「書き出し」
17で割ると3余り、23で割ると7余る整数のうち、小さい方から5番目の整数を求めなさい。
17で割ると3余る数(17で割ると14不足する数)、23で割ると7余る数(23で割ると16不足する数)は、余りも不足も一致しませんね。
そこでまずはどちらか一方を“書き出し”てみます。
ここでは23で割ると7余る数を書き出してみると、7,30,53,76,99,122,…
122は17で割ると3余る数でもあるので、共通する数の最小が見つかりました。
その後は以下のイメージのように、

17と23の最小公倍数391を加えていけば、つねに17で割ると3余る数でもあり、23で割ると7余る数であるものが見つかりますね。5番目なので、
122+391×4=1686となります。
「余りがいくつかわからない」
74個のみかんと100本のバナナと165個のりんごをそれぞれに同じ数ずつできるだけ多くの子供に分けようとしたところ、同じ数だけ余りました。子供は何人いましたか。
【問1】同様に“余り”が同じですが、それがいくつかはわかっていません。
同様に“線分図”でイメージしてみましょう。
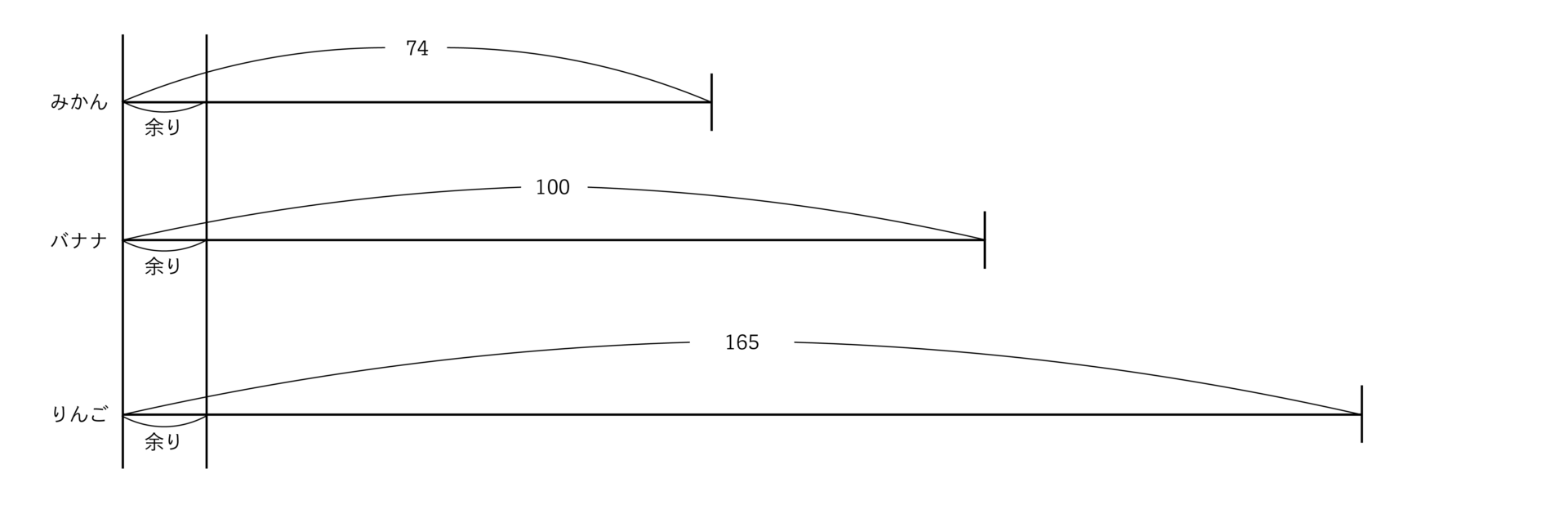
“線分図”の左端の余りを同じにするためには、右端から以下のように同じ数で分けていくと、差にあたる26や65を割り切れなければいけないことがわかります。
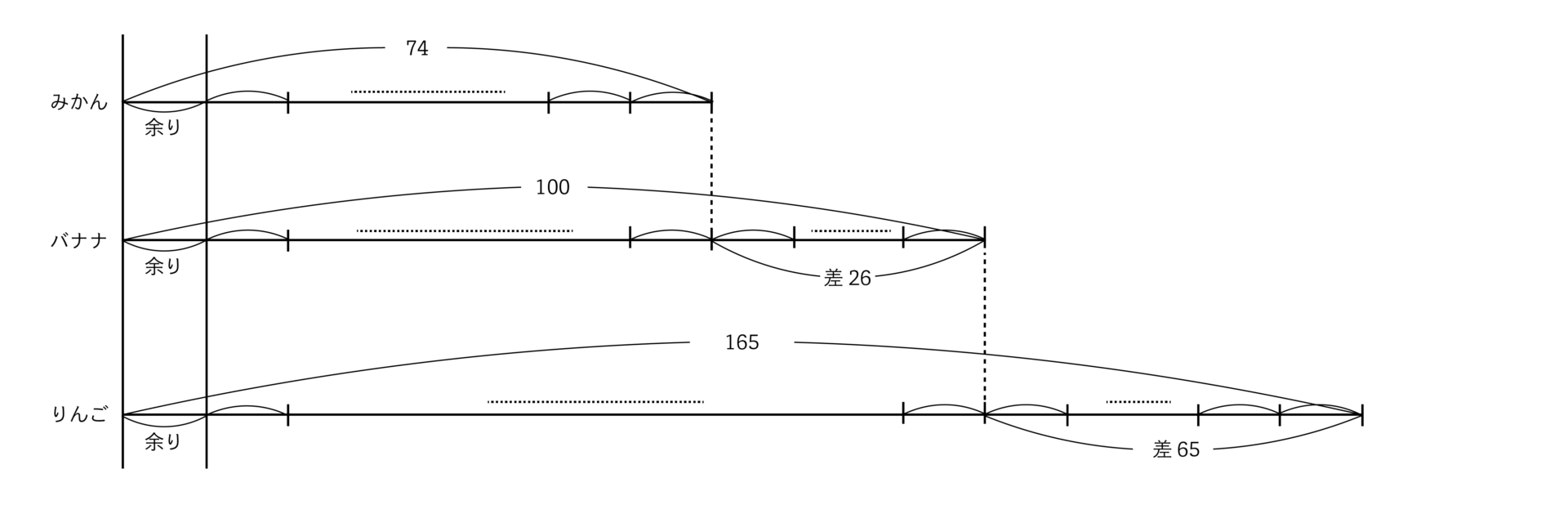
“できるだけ多くの子供にに分ける”ことから、26と65の最大公約数にあたる13人が正解です。
しかしながら、学び始めの時期や苦手となってしまった場合等、たんにパターン演習として扱うのではなく、上記のような“線分図”等を利用して意味をしっかりつかむことが大切です。
こういったパターン演習だけではない“理解する”“意味を知る”学習こそが応用力を生んでいきます。
「余り」に関する問題の多様な広がり
次の計算の結果を9で割ったときの余りを求めなさい。1234567+2345671+3456712+4567123+5671234
“余り”に関する問題はさらに様々な広がりを見せています。この【問5】のような問題では“余りの和(積)”といったものがテーマとなります(高校数学では“合同式”とよばれる考え方となっていきます)。
小さな数で確かめる
もう少し小さな数で実験してみましょう。
「567は9で割り切れますか?」
もちろんそのまま割り算をしても567は9で割り切れることがわかりますが、皆さんご存知の「倍数判定法」において“9の倍数は『各位の和が9の倍数』”でしたね。よって、
5+6+7=18 ⇐9の倍数(9で割り切れる)
それでは、
「568を9で割ると余りはいくつ?」
こちらももちろんそのまま割り算をしても、568を9で割ると1余ることがわかりますが、上記のような「倍数判定法」を利用すると、
5+6+8=19 19÷9=2…1
と1余ることがわかりますね。
さらに足し算をしてみます。
「568+568の計算結果を9で割ると余りはいくつ?」
568+568=1136
1136÷9=126…2
もちろん上記のように実際に足した数を9で割ると余りが2であることがわかりますが、ここで“余りの和”に注目してみると、
568(5+6+8=19 19÷9=2…1)は、9で割ると余りが1であることが「倍数判定法」でわかっているので、余りの1と余りの1を足して計算結果の余りは2と求めることができます。
【問5】を計算してみる
したがって、【問5】は一つずつの数が全て
1+2+3+4+5+6+7=28 28÷9=3…1
と余りが1とわかりますので、
計算結果は1+1+1+1+1=5と求められます。
具体的に試行錯誤しつつ、自然に吸収する
このように“具体的”に試行錯誤しつつ、自然に知識として吸収することが、より高いレベルの問題に太刀打ちできる基本行動となりますね。



















