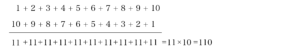前回までの「数の性質」に引き続き、ここからの２回は「規則性」を扱っていきたいと考えています。
その２回を“数列”と“周期”に分けて、その第一弾として今回は“数列”を取り上げます。
規則的に並んだ数の列を“数列”と呼びますが、中学入試でも取り上げられる主だったものを問題とともにご紹介していきます。
しっかり成り立ちを理解することで、よくありがちな“公式当てはめ”にならないようにしていきましょう。
等差数列（と和）の考え方
あるきまりにしたがって、つぎのように数がならんでいます。
$5, 9, 13, 17, 21, 25, 29, \cdots$
①$20$番目の数は何ですか。
②$20$番目までの和はいくらになりますか。
隣り合う$2$つの数の差（公差$=4$）が等しい“等差数列”ですね。
20番目の数を考える方法
$20$番目の数は最初の数（初項）$5$に差（公差）の$4$を$19(20-1)$回加えれば求めることができますね。よって、
$5+4\times (20-1)=\underline{81}$ …①
となります。
「等差数列の和」の考え方
②の“等差数列の和”についても考えてみましょう。
求め方を知っているという人も多いと思いますが、ここではあの世界三大数学者の一人でもある“ガウス”が少年時代に先生から出された問題
を“$1$から$10$までの和”と小さくした場合で考えてみましょう（ちなみにガウス少年は$1$から$100$までの和を一瞬で$5050$と答えたそうですよ）。
ガウス少年はどうやって考えたのでしょうか。
$1+2+3+4+5+6+7+8+9+10$の下に逆さ向きで$10$～$1$の和を並べ、それぞれの列を縦に足してみます。すると、
と、全ての列の和が$11$ずつとなり、それが$10$列あることがわかりますね。
ちなみにこの一列ずつの和$11$は、初項の$1$と末項の$10$の和となっており、列の数$10$は並んでいる数の個数となっています。また全体の和$110$は、$1$～$10$（$10$～$1$）の和$2$段分ですから求めたい$1$～$10$の和は、$110\div 2＝55$ですね。
ここから“等差数列の和”の求め方が、「（初項$+$末項）$\times$個数$\div 2$」となっているんですね。
よって②の問題では、
$(5+81)\times 20 \div 2＝860$となります。
さて、上記の“等差数列”の中でも以下のような奇数だけが並んでいる場合を見てみましょう。
$1, 3, 5, 7, 9, 11, 13, \cdots$
この数列も公差が$2$の“等差数列”なので、$20$番目を求めたければ、$1+2\times (20-1)=39$となり、$20$番目までの和は、$(1+39)\times 20\div 2＝400$と求めることができます。
等差数列の計算における「別の考え方」
一方でこんな考え方もあります。以下のように偶数とペアにして並べてみると、
偶数の$20$番目は$2\times20=40$で、その列の上が奇数の$20$番目ですから$40-1=39$と求めることもできますね。また和については以下のように「○」を並べて見てみると、
のように、「○」が正方形の形を描いていくことがわかります。そこで、
$1=1\times 1\\
1+3=2\times 2\\
1+3+5=3\times 3\\
1+3+5+7=4\times 4\\
\cdots$
と求めることができ、$1+3+5+\cdots +39=20\times 20=400$となりますね。
階差数列の考え方
あるきまりにしたがって、つぎのように数がならんでいます。
$3, 4, 6, 9, 13, 18, 24, \cdots$
$20$番目の数は何ですか。
等差数列と違い、隣り合う２つの数の差が等しくありません。
$20$番目の求め方は簡単ですね。初項が$3$ですので$20$番目を求めたければ、
$3+(1+2+3+ \cdots +19)=3+(1+19)\times 19\div 2=\underline{193}$
と、間の差の部分の和を“等差数列の和”の求め方を利用すればよいですね。
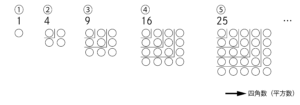
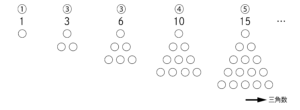
「三角数」「四角数（平方数）」
ところで以下のような“階差数列”は、「○」で表すときれいな形となっていることから、“三角数”や“四角数（平方数）”といった呼ばれ方もします。
等比数列（の和）の考え方
次の計算をしなさい。
① $10+20+40+80+160+320$
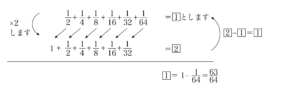
② $\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}$
③ $\frac{1}{3}+\frac{1}{9}+\frac{1}{27}+\frac{1}{81}+\frac{1}{243}+\frac{1}{729}$
隣り合う数を見てみると、今までのように注目すべきは“差”ではないようです。
等比数列の和を求める
それではその和を求めてみましょう。
①ではそのまま前から順番に足してもたいして時間はかからなさそうですが、②や③を求める時のために（通分して求めると大変そうです）、以下のように工夫してみましょう。
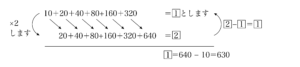
１の式を$2$倍した２の式から１をひけば１が求められるというわけですね。
その際、$20+40+80+160+320$は同じ値なのでひくと$0$になりますね。
同様に②、③もやってみましょう。
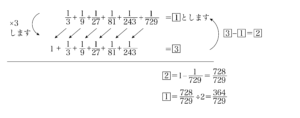
③の問題は、下の段から上の段をひいた値は求めたい答えの２つ分に当たっていることに注意しましょう。
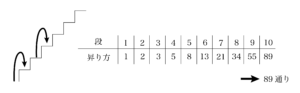
フィボナッチ数列の考え方
次のようなきまりで数がならんでいます。
$1, 1, 2, 3, 5, 8, 13, 21, \cdots$
$15$番目の数を求めなさい。
今までの数列と違って、差や倍数関係に関連した数列ではありませんね。
さて問題の15番目の数を、規則に従って求めてみると、
$1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, \underline{610}$
となりますね。
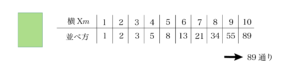
中学入試においても以下のように“フィボナッチ数列”があらわれるたくさんの出題例が見られます。
中学入試における「フィボナッチ数列」の出題例
$1$歩で$1$段上がる昇り方と、$1$歩で$2$段上がる昇り方の$2$種類があるとき、階段の$10$段目までの昇り方は何通り？
$2m \times 1m$の畳を何枚か使って、「たて$2m \times$横$\rm{X}$$m$」の部屋に並べる時、「たて$2m \times$横$10m$」の部屋に並べる並べ方は何通り？
こういった問題に対する“取り組み方・手順”といったものは、あらためて記事にしたいと思っています。
次回は「規則性②」として“周期”を扱いたいと思います。お楽しみに！
