これまで様々な中学受験算数単元学習に関して記してきました。その単元学習の最後の締めくくりとして「場合の数」を扱っていきます。
場合の数を求めるとは、“あることがらの起こり方が何通りあるかをかぞえること”で、以下のようなものが例となります。
“表”“裏”の2通り
“1”“2”“3”“4”“5”“6”の6通り
場合の数を求める――その1「場合分け」
まずはこの「場合の数」の中で、“表”や“樹形図”といったものを用いてしっかり調べていく方法を見てみましょう。
この場合の数を学ぶにあたっての初期段階において、以下のようにしっかり書いて求めることをしていたかどうかがその後の成否を分けるといっても過言ではありません。その際、ただやみくもに調べるだけではなく“場合分け”を意識して取り組んでいくことが大切ですね。
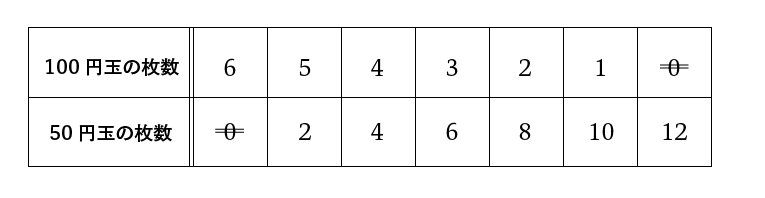
50円玉と100円玉を使って、ちょうど600円はらう方法は何通りありますか。ただし、50円玉も100円玉も1枚以上使うものとします。
以前の記事の中でも“整理”方法についてお伝えしたことがありましたが、こういった何通りあるかを調べる際にも“表”等を利用して整理することが大切です。ちなみに大きい方の100円玉の枚数で“場合分け”するのがポイントですね。
5通り
樹形図を利用する
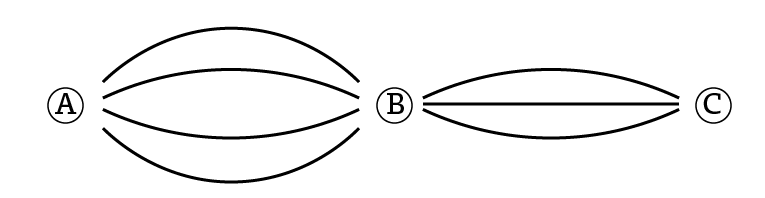
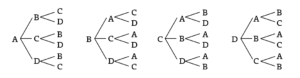
6年生ともなれば“積の法則”によって式を用いて求めることにもなりますが、ここでもやはり“整理”することをテーマとし、その整理方法の一つである“樹形図”を利用します。ここでも“場合分け”するのがポイントとなりますね。
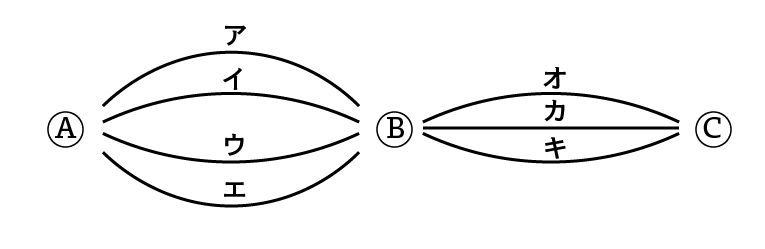
まずはそれぞれの道に記号をつけます。
A~Bをどの道を使うかで“場合分け”します。
A~Bでアを使うときの“樹形図”をかいてみると、
全てかいてもよいのですが、A~Bではアも含めてイ、ウ、エと4通りの場合があります。A~Bでアを使った上の“樹形図”同様に3本枝分かれしたものが4通りありますので、
$4 \times 3=12$(通り)
の行き方がありますね。
その際“場合分け”を意識して取り組むことが、“計算”ですぐに解くことが難しい問題に出会った時に大きな力を発揮することとなります。
場合の数を求める――その2「順列」
「場合の数」を学習する中で出てくる問題で“順列(並べ方)”や“組み合わせ(選び方)”といったものがあります。
前項では“場合分け”をお伝えすることをテーマとしましたので、“表”や“樹形図”を用いて書き出すことで求めていきましたが、ここからは主に“計算”を用いて求めていくことにします。その中にも“場合分け”のような大切な考え方がありますので、是非活用していってほしいと思います。
いくつかのものを一列に順序を考えて並べる「順列」
まずは“順列(並べ方)”です。順列とは“いくつかのものを一列に順序を考えて並べること”で、この並べ方を考える問題を“順列の問題”といいます。
例えば以下のような問題です。
A, B, C, Dの4人から3人選んで一列に並べる並べ方は何通りありますか。
“樹形図”を頭に思い浮かべながら計算してみると、
と求めることができますが、人が並ぶ場合だけではなく以下のように様々な場面に同じ考え方を応用することができます。
カードを並べる問題
1 , 2 , 3 , 4 の4枚のカードで3けたの整数を作ります。全部で何通りできますか。
一見すると別のように見える問題でも、“言い換え”ることによって全く同じ考え方で求められることが多々あります。特にこの「場合の数」の問題ではこの“言い換え”る力が大変重要です。
1のカードをA、2のカードをB、3のカードをC、4のカードをDと“言い換え”ると、(例)の問題と全く同様の考え方で求めることができますね。よって、
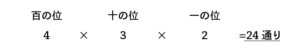
色分けの問題
こちらも赤をA、青をB、黄をC、黒をDと“言い換え”ると、やはり(例)の問題と全く同様の考え方で求めることができますね。よって、
「表せる大きさ」の問題も順列に言い換える
次のような問題も“順列”の考え方に“言い換え”ることができます。
さいふの中に50円玉が3個、10円玉が2個、1円玉が1個はいっています。この6個のお金を使っておつりなしで支払うことのできる金額は全部で何通りありますか。
ただし、50円玉0枚、10円玉0枚、 1円玉0枚では0円になってしまうため、
$24-1=23$(通り)
場合の数を求める――その3「組み合わせ」
“順列(並べ方)”に続き、“組み合わせ(選び方)”について考えてみましょう。
組み合わせとは“いくつかのものの中から何個かを取り出してできるグループの数を求めること”で、順列のように並べる順序は考えません。このような問題を“組み合わせの問題”といいます。例えば以下のような問題です。
A, B, C, Dの4人から3人のそうじ当番を選ぶ選び方は何通りありますか。
順列の時と比較して求めてみましょう。まずは“樹形図”を用いて4人から3人選んで並べてみると、
これを“計算”で求めたものが、順列の例にもあった、
$4\times 3 \times 2=24$(通り)
でしたね。
ところが“組み合わせ(選び方)”では、
A―B―C
A―C―B
B―A―C
B―C―A
C―A―B
C―B―A
のように、(A, B, C)3人が並んだ場合の6通りは全て同じ3人を選んだことになりますので、1通りとなりますね。つまり、
$4 \times 3 \times 2=24$(通り)の並べ方に対し、それぞれ6通りが同じ選び方になっているので、
$(4 \times 3 \times 2) \div 6 = 4$(通り)
となります。
ちなみにこの6通りは、選んだ3人の並べ方にあたりますので次のような式に表すことができます。
$(4 \times 3 \times 2) \div (3 \times 2 \times 1) = \frac{(4 \times 3 \times 2)}{(3 \times 2 \times 1)} =4$(通り)
さらに、ここでも“言い換え”を用いてみたいと思います。
“4人から3人のそうじ当番を選ぶ”は、“4人からそうじ当番以外の1人を選ぶ”ことと“言い換え”ることができますね。つまり、
AかBかCかDの1人を選ぶ4通り
と求めることもできますね。
「総当たり戦」の問題
それではこの“組み合わせ(選び方)”でも様々な場面に応用してみましょう。
A, B, C, Dの4チームがどのチームとも1回ずつ試合をすると、試合数は全部で何試合ですか。
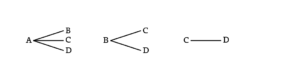
どんな試合が行われるのか、樹形図で見てみましょう。
上の6試合があることがわかりますが、これもよく見て“言い換え”てみると、“A, B, C, Dの4チームから試合する2チームの選び方”となりますね。
よって先ほどの(例)にもあった“計算”方法を用いてみると、
$(4 \times 3) \div (2 \times 1)=\frac{(4 \times 3 )}{(2 \times 1)} =6$(試合)
と求めることができました。
「三角形の個数」の問題
まだまだ“言い換え”ることによって、“組み合わせ(選び方)”として求められる問題は多々あります。
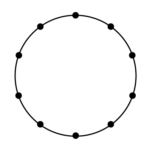
円周上に10個の点があります。このうちの3つの点を直線で結んでできる三角形は何個ありますか。
10個の点から3個の点を選ぶ選び方
$(10 \times 9 \times 8) \div (3 \times 2 \times 1) = \frac{10 \times 9 \times 8 }{3 \times 2 \times 1} = 120$(通り)
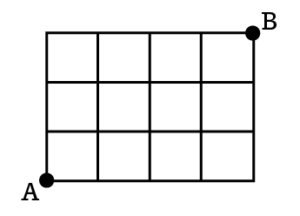
「最短経路」の問題
AからBまでの最短経路は、縦の辺を上に3つ(↑↑↑)、横の辺を右に4つ(→→→→)進めばよいので、
↑ ↑ ↑ → → → →
$(7 \times 6 \times 5) \div (3 \times 2 \times 1) =\frac{7 \times 6 \times 5}{3 \times 2 \times 1} = 35$(通り)
「碁石の並べ方」の問題
白い碁石が2個と黒い碁石が4個あります。この6個の碁石を全部使って横1列に並べると並べ方は何通りありますか。
一見すると“順列(並べ方)”の問題のように見えますが…。
〇 〇 ● ● ● ●
$(6 \times 5) \div (2 \times 1) =\frac{6 \times 5}{2 \times 1}=15$(通り)
「仕切り」を活用する
6個のリンゴをA, B, C 3人に分ける分け方は何通りありますか。ただし3人とも1個以上はもらうものとします。
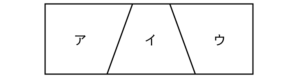
“仕切り”を利用してみると、
上の図では2つの仕切りでAが1個、Bが2個、Cが3個を表していますね。
つまり、5か所の“間”の場所から2か所の“仕切り”を置く場所を選ぶ選び方ですね。
$(5 \times 4) \div (2 \times 1) = \frac{5 \times 4}{2 \times 1} = 10$(通り)
今回は「場合の数」をテーマに取り上げましたが、算数の中でも大変有意義に頭を働かせることで、求める“コンパクトさ”や“スピード感”(“充実感”や“達成感”も)が違ってくる単元かと思います。
その際には上記の例にあったような“場合分け”や“言い換え”といったことを常に意識してみてほしいと思います。