その1「余事象」
前回様々な基本の「場合の数」を扱ってきましたが、その中で“場合分け”や“言い換え”といった有意義な頭の働かせ方で“コンパクトさ”や“スピード感”“負担感”が多いに違ってくることがわかったことと思います。
そういった有意義な考え方の中で、さらにもう一つ、目的の場合の数を求めるのに複数の場合分けをしなければいけないなど、手間がかかりそうな問題では「余事象」という考え方を利用してみましょう。
例えば以下のような問題です。
大中小$3$個のサイコロをふるとき、少なくとも$1$個は$4$の目が出る場合の数を求めなさい。
余事象＝ある事象に対してそれが起こらない事象
「余事象」とは“ある事象に対してそれが起こらない事象のこと”をいいます。
もし“少なくとも1個は4の目が出る”を直接考えると、大だけが4の目の場合、中と小が4の目の場合……など、いろいろな場合に分けて考えなければなりませんね。このようなときに余事象の考え方が利用できます。“少なくとも1個は4の目が出る”の余事象は“1個も4の目が出ない”ですね。これなら場合分けして考える必要もなさそうです。この余事象をすべての場合から除きましょう。
大中小のサイコロの目の出方すべての場合の数は、
$6 \times 6 \times 6 = 216$（通り）
1個も4の目が出ない、つまり大中小のサイコロの目が$1，2，3，5，6$のどれかになる場合の数は、
$5 \times 5 \times 5 = 125$（通り）
よって、$216 - 125 = 91$（通り）
例題を通して「余事象」の考え方を確認する
さらに、いくつかの問題を見てみましょう。
$1, 2, 3, 4, 5, 6$の$6$個の整数の中から「$3$と$5$」のように連続していない$2$個の整数を取り出します。取り出し方は何通りありますか。
$1$～$6$の$6$個から“$2$個の整数”を取り出すときのすべての取り出し方は、
$（6 \times 5） \div （2 \times 1） = \dfrac{6 \times 5}{2 \times 1} = 15$（通り）
“連続していない”ものを求めたいので、連続する整数の取り出し方をここから除きましょう。
これは「$1$と$2$、$2$と$3$、$3$と$4$、$4$と$5$、$5$と$6$」の$5$通りありますね。
よって、$15 - 5 = 10$（通り）
図形の問題で「余事象」を活用する
図のように三角形$\rm{ABC}$の$3$辺$\rm{AB}, \rm{BC}, \rm{CA}$上に点をそれぞれ$2$つ、$3$つ、$4$つとります。この$9$つの点の中から$3$つとり、その$3$点を頂点とする三角形を作ります。三角形は全部で何通りできますか。
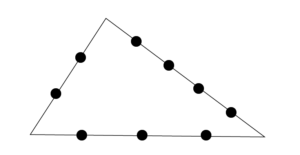
$9$つの点から$3$つを選べば三角形ができそうですが、同じ辺上から$3$点を選んでも三角形にはならないので、その場合を除きましょう。
$9$つの点から$3$つを選ぶ選び方は、
$（9 \times 8 \times 7） \div （3 \times 2 \times 1） =\dfrac{9 \times 8 \times 7}{3 \times 2 \times 1} = 84$（通り）
BC上から$3$点の選び方が$1$通り、CA上から$3$点の選び方が$4$通り、
よって、$84 - （1 + 4） = 79$（通り）
その2「前の場合利用」
以前の記事（「規則性」）の中で“フィボナッチ数列”を取り上げたことがありました。
その際には問題例として取り上げただけでしたが、今回は結果としてではなく、“取り組み方・手順”について記していきたいと思います。算数の問題に取り組む際、場合の数の単元のみならず大変大切な考え方となります。
以下のような問題が与えられた時、皆さんはどのように取り組んでいくでしょう？
$1$歩で$1$段上がる昇り方と、$1$歩で$2$段上がる昇り方の$2$種類があるとき、階段の$10$段目までの昇り方は何通り？
ややもすると、“$1$段, $1$段, $1$段, $1$段, $1$段, $1$段, $1$段, $1$段, $1$段, $1$段で1通り目”、“$1$段, $1$段, $1$段, $1$段, $1$段, $1$段, $1$段, $1$段, $2$段で$2$通り目”……なんてことになりがちです。こういった場合どのように取り組んでみたら良いでしょう？
まずは「小さな場合で実験」してみる
まずは“小さな場合で実験”してみましょう。つまり、いきなり$10$段の場合を求めようとするのではなく、“小さな場合”すなわち$1$段目まで昇るところから調べ、何か規則性がないかどうか“検証”するといった具合です。
$1$段目までの昇り方は$1$通り、$2$段目までの昇り方は“$1$段$+ 1$段”か“$2$段”の$2$通りですね。$3$段目までの昇り方は“$1$段$＋ 1$段$＋ 1$段”か“$1$段$＋ 2$段”か“$2$段$＋ 1$段”の$3$通りありますね。
ここで一旦立ち止まって“検証”してみましょう。
$3$段目までの昇り方は“はじめ１段⇒その後２段”、この時は$2$段の昇り方で$2$通り、“はじめ２段⇒その後１段”、この時は$1$段の昇り方で$1$通り。つまり“前の場合（ここでは$1$段目までの昇り方と$2$段目までの昇り方の和”になっていますね。
すると4段目までの昇り方は“$2$段目までの昇り方と$3$段目までの昇り方の和”で、
$2 + 3 = 5$（通り）
となり、まさに“前$2$つの数を加えると次の数になる”という“フィボナッチ数列”があらわれます。
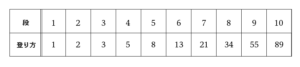
続きを表にして整理してみましょう。
よって、$89$通り
知識として暗記するのではなく、「思考法」として取り組む
結果として“有名な”数列があらわれることになりましたが、ここで大切なのは知識として暗記することではありません。算数・数学に取り組む際の“思考法”として、上記の例のような取り組み方を是非行ってほしいということです。
今回は以下問題例として“有名な”ものを取り上げますが、こういった“思考法”を利用する問題は問題例以外にもたくさんの出題があります。いずれ「応用編（入試実践編）」として取り上げたいと思っています。
たて$2\rm{cm}$, 横$1\rm{cm}$の長方形のタイルがたくさんあります。このタイルをすきまなく並べて、たて$2\rm{cm}$, 横$10\rm{cm}$の長方形を作るとき、タイルの並べ方は何通りありますか。
（例）と同様に、いきなり横$10\rm{cm}$の場合を求めようとするのではなく、まずは“小さな場合で実験”してみましょう。
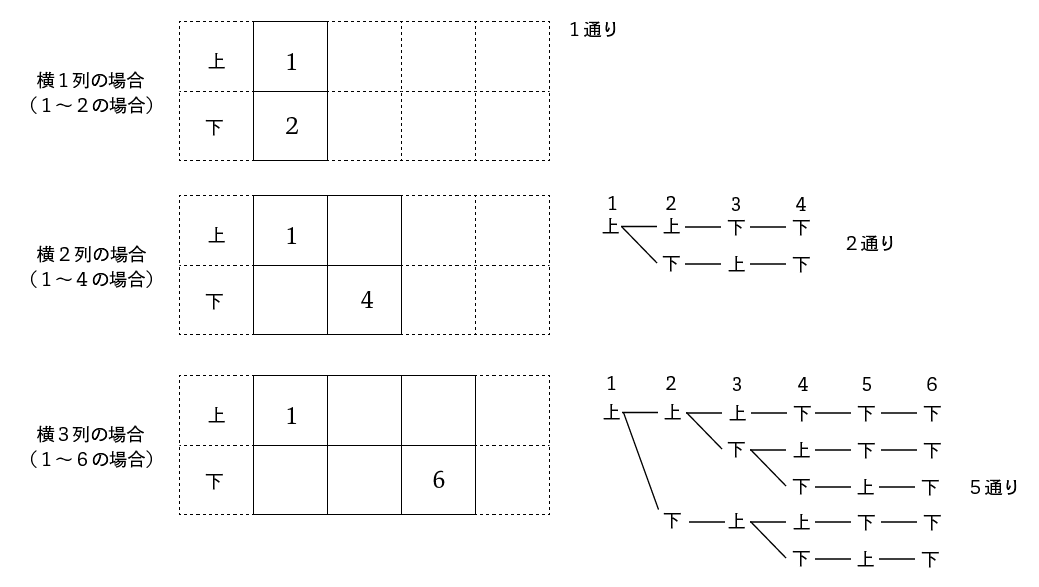
横$1\rm{cm}$の場合は$1$通り、横$2\rm{cm}$の場合は以下のように$2$通りですね。
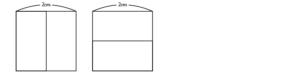
それでは横$3\rm{cm}$の場合はどうでしょう。左はしを上の$2\rm{cm}$の場合で求めた$2$つの場合で“場合分け”しましょう。すると、
やはり（例）と同様に“前の場合（ここでは横が$1\rm{cm}$の場合と横が$2\rm{cm}$の場合）の和”になっていますね。$1 + 2 = 3$（通り）
すると、横が$4\rm{cm}$の場合のタイルの並べ方は“横が$2\rm{cm}$の場合と横が$3\rm{cm}$の場合の和”で、
$2 + 3 = 5$（通り）
となり、まさに“前$2$つの数を加えると次の数になる”という“フィボナッチ数列”があらわれます。
表にして整理してみましょう。
よって、$89$通り
カラタン数
オオカミ$3$匹とヒツジ$3$匹が別々のおりに入っています。いまこの$6$匹を$1$匹ずつ$1$つの同じおりに入れたいのですが、オオカミの数がヒツジの数より多くならないようにしたいです。入れ方は何通りありますか。
この問題においても、ややもすると“えっ～と、最初にオオカミは入れられないから$1$匹目はヒツジ、次はオオカミを入れてもヒツジを入れてもO.K.……”のように、やみくもになりがちです。
やはりまずは“小さな場合で実験”してみましょう。
オオカミ$1$匹、ヒツジ$1$匹のときは、
オオカミ$2$匹、ヒツジ$2$匹のときは、
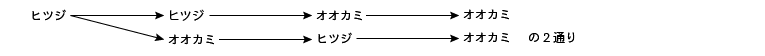
オオカミ$3$匹、ヒツジ$3$匹にいく前にここで一旦“検証”してみましょう。
左から右に順におりに入れていくことを上記の樹形図のように書く際、“ヒツジ→オオカミ→ヒツジ→オオカミ”など、左のヒツジよりも右のオオカミの数が多くなってしまわないようにかかなければいけません（“ヒツジ→オオカミ→オオカミ→ヒツジ”等はいけませんね）。
こういった“一方の個数が他方の個数をこえないようにする”場合の数であることに気が付くと、“道順解法（カタラン数）”が利用できることにつながります。
カラタン数を考える際に用いる図
下の図を見てください。
この図はどの道順でも“ヒツジ”の数を“オオカミ”の数がこえないようになっているので、図の“右に進む”を“ヒツジ”の数、“上に進む”を“オオカミ”の数に当てはめると、こういった問題を解くのに使えるのです。
上記の問題に応用すると、スタートから右の方向へ$1$マス進むと“ヒツジ”の数が$1$つ増えることをあらわし、上の方向へ$1$マス進むと“オオカミ”の数が$1$つ増えることをあらわします。
例えばオオカミ$2$匹、ヒツジ$2$匹の場合を見てみましょう（樹形図と照らし合わせてください）。
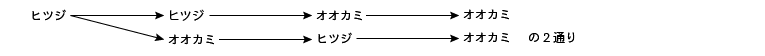
ヒツジは$1$つから$2$つまで（右方向へ$1$マスから$2$マスまで）進むことができます。ヒツジが$1$つだけ（図のア）増えたときはオオカミは$1$つだけ（図のイ）しか増やすことができません。オオカミを$2$つまで増やしてしまうと、オオカミがヒツジの数をこえてしまいますよね（図のウ）。
したがってオオカミ$2$匹、ヒツジ$2$匹の場合はヒツジが$2$マス、オオカミが$2$マスあるので、図のエの地点までということになり、「最短経路の道順」は$2$通りあるということがわかります。
上記の問題のオオカミ$3$匹、ヒツジ$3$匹の場合、図のように“道順解法”を利用するとあっさりと求めることができます。ヒツジが$3$マス、オオカミも$3$マスあるので、$5$通りです。
右のマス目に、$1$から$8$までのすべての整数をあてはめた表を作ります。
左隣の数より大きく、真下の数より小さくなるようにあてはめた表は全部で何通りできますか。
こちらもまずは$2$マス、$4$マス、$6$マスの“小さな場合で実験”してみましょう。
そしてこの樹形図のかき方を“検証”してみてください。
左から右に順に樹形図をかいていく際“上→上→下→上→下→下”など、左隣の数より大きく、真下の数より小さくなるようにかいていくと、“どの通りのどのタイミングでも‘下’の個数が‘上’の個数をこえない”ようになっていることに気がつきます（$1$～$3$をかく段階で“上→下→下”となってしまうのは、“下”の個数が“上”の個数をこえてしまうのでありえない）。
[問4]同様、“どの通りのタイミングでも‘下’の個数が‘上’の個数をこえないようにする”ことに気がつくと、“道順解法（カタラン数）”が利用できることにつながります。
完全（攪乱）順列の問題
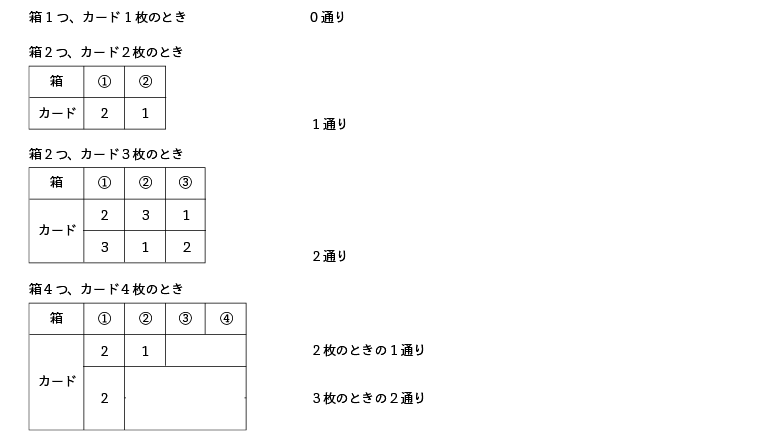
箱が5個あり、それぞれ$1, 2, 3, 4, 5$と番号がつけてあります。この箱の中に$1, 2, 3, 4, 5$と番号のついたカードを$1$枚ずつ入れました。
カードの番号と箱の番号が全く一致しないような入れ方は何通りありますか
“完全（攪乱）順列（整数$1, 2, 3,\cdots \cdots, n$において、$i$番目が$（i \leqq n）i$でない順列）”の問題で、その総数は“モンモール数”とよばれます。とはいえはじめからそれがわかっているわけではありません（今後は是非知識として身につけてしまいましょう）。
これまで同様“小さな場合で実験”してみます。
前の場合（$2$枚のときの$1$通りと$3$枚のときの$2$通り）が出てきました。箱①に$2$のカードを入れた場合が合わせた$3$通り、そして上記の①に$2$を入れた場合以外に①に$3, 4$のカードを入れた場合があるので、
$（1 + 2） \times 3 = 9$（通り）
やはり前の場合（$3$枚のときの$2$通りと$4$枚のときの$9$通り）が出てきました。箱①に$2$のカードを入れた場合が合わせた$11$通り、そして上記①に$2$を入れた場合以外に①に$3, 4, 5$のカードを入れた場合があるので、
$（2 + 9） \times 4 = 44$（通り）
ちなみにこの“前の場合を利用”することで、
箱$6$つ、カード$6$枚のときは、
$（9 + 44） \times 5 = 265$（通り）
と求めることができます。
次回はこの「前の場合利用」の問題のような“算数（数学）的思考力”の問題を、場合の数の単元の中からご紹介したいと思います。お楽しみに！
