その1「小さな場合で実験→前の場合利用」
前回の「場合の数②」の後半、「前の場合利用」のような“算数(数学)的思考力”を利用する有名な問題について記しました。
“算数(数学)的思考法”として最も大切なことは“取り組み方・手順”です。その際、最初に行うべき行動として前回も行った“小さな場合で実験”してみましょう。そしてその実験結果を適当にメモするのではなく、しっかり「表」に整理していくことが重要です。
実験結果を「表」で整理する
$1$秒後には以下の通り、$\rm{B}, \rm{C}, \rm{D}$に$1$通りずつの動き方があります。
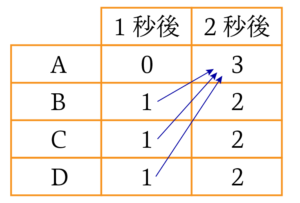
さらに$2$秒後に頂点Aにあるような動き方は、手前の1秒後の時に$\rm{B}, \rm{C}, \rm{D}$にいればよいので、以下のように$3$通りとなります。また$2$秒後に$\rm{B}$や$\rm{C}$や$\rm{D}$にあるような動き方は、$2$通りずつとなりますね(例えば頂点$\rm{B}$にあるような動き方は、手前の$1$秒後に$\rm{A}$か$\rm{C}$か$\rm{D}$にいればよいので、$2$通りですね)。
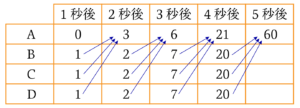
$5$秒後に点$\rm{P}$が頂点$\rm{A}$にあるような動き方は、$60$通り
「思考力」を見るための大きな流れ
さらに、レベルが高い難関とよばれる中学校が求める“思考力”を見るための大きな流れが以下のようなものです。
次の問題ではその“思考の流れ”といったものを見ていきましょう。
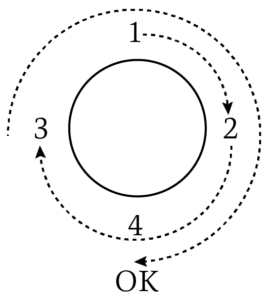
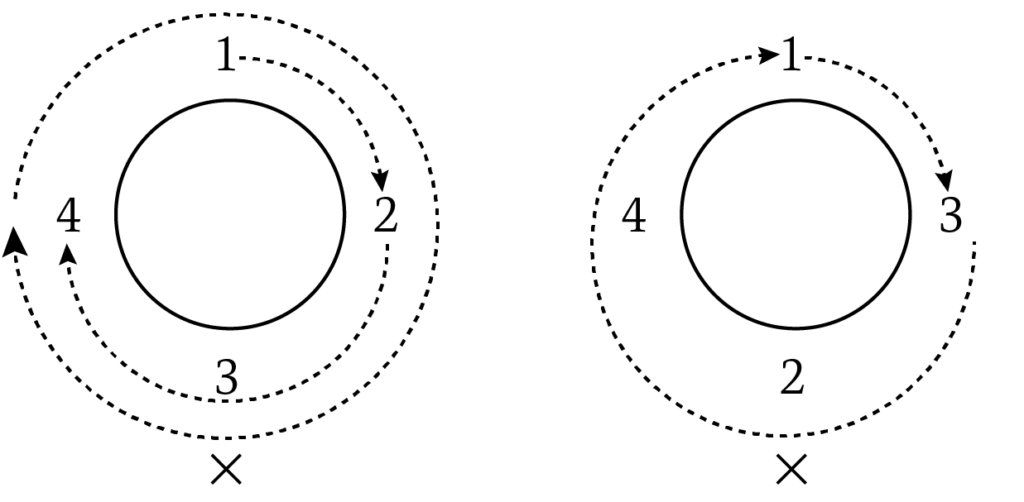
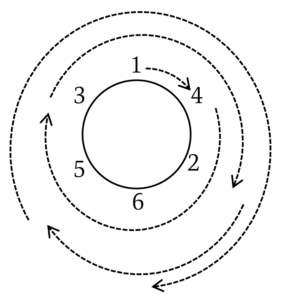
図のように円周に沿って等間隔に$1$から$4$までの$4$個の整数をひとつずつ並べます。$1$からスタートして$1$だけ時計回りに進んで$2$に、以下同様に$2$から$2$だけ進んで$3$に、$3$から$3$だけ進んで$4$に進みます。このとき$2$から$4$までのすべての整数にちょうど一度ずつ到達することができます。
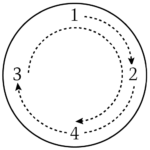
上のように$1$から$\rm{A}$までの整数を等間隔に並べ、$1$からスタートして、$1$だけ時計回りに進み、以下同様にそのとき到達した整数からその数だけ時計回りに進みます。このとき、やはり、$2$から$\rm{A}$までのすべての整数にちょうど一度ずつ到達することができるようにします。
(1)$\rm{A}=6$のとき、最後に到達する整数はいくつですか。また、このとき$1$の真向かいに並んでいる整数はいくつですか。$1$から$6$までの$6$個の整数のこのような並べ方をひとつ書きなさい。
(2)$\rm{A}=7$のとき、$1$から$7$までの$7$個の整数をこのように並べることはできません。その理由を説明しなさい。
確かに“何だろう?”と思わせる問題のスタートですね。その際ただやみくもに問題を読むだけではなく、問題文や例の時点で試行検証してみましょう。
問題文では以下の図のような並べ方はO.K.となることが記されています。
問題文や例から少なからず「何か」をつかんでおく
さあ、皆さんならばこの時どういった行動をするでしょう?
いきなり(1)に進みますか?
そういったお子様も多いことでしょう。しかも並べ方を“ひとつ”かくだけならば、6年生でなくともできるお子様も多いと思います。しかしながらこの時点で(1)に進んでしまうと、(1)の問題においてもたくさんの場合を“試行”しなければいけませんね。
そこで問題文や例の時点で少なからず“何か”をつかんでおきましょう。
上の2つのような並べ方では全ての整数に到達することはできないですね。
試行によって得られた検証結果
さてこれらの“試行”からいったい何を“検証”できたでしょう?
(1) の問題と合わせて考えてみると、どうも“最後”の数が注目すべき数のようです。
問題文の例では「$4$」が最後の数ですね。先ほどまでの$3$回の“試行”において最後の「$4$」がどんな動きになるかわかりましたか?
そうです。最後の「$4$」に到達すると、必ず一周回って同じ「$4$」に戻ることになりますね。したがって「$4$」は最後に到達しなければなりません($2$番目の例のように途中をすっとばしてしまうことになります)。よって(1)では最後に到達する整数は「$6$」ということになります。
もう一つの検証結果
これだけでも十分“検証”できていますが、さらに(2)のことまでを考えた場合、もう一つ“何か”が検証できるとすばらしいですね。
その一つとは、最後の「$6$」にたどり着く前までに“$1$から$5$までの和”だけ進んでくるというものです($1$から$5$がどのように並んでいても「$6$」にたどり着くまでには、$1 + 2 + 3 + 4 + 5 = 15$進んできますよね)。
したがって$1$から$15$進んだ場所は、$15 \div 6 = 2 \cdots 3$
$2$周回って$3$進んできた(つまり$1$の真向かい)ところに「$6$」があるわけです。
並べ方の例の一つが以下のようなものです。
このような“検証”ができると(2)以降の進み方が俄然変わります。
(2)の問題の考え方
もし何も“検証”なしにここまで進んでしまうと、(1)において問われている“最後”や“$1$の真向かい”ということも全く関係なしに、“やみくもに”当てはめることになってしまいますね(とはいえ、そうであっても(1)が正解したお子様はすばらしい!)。さらに(2)に至っては、また一から“やみくも”に“試行”することになってしまいます(さすがに時間的にも厳しいですよね)。
ちなみに(1)までに上記2つのこと(①最後の数は最後に到達しないといけない ②それまでにその手前までの和だけ進む)が“検証”できていると、(2)はかなりスムーズでコンパクトにできますね。最後の「$7$」は最後に到達しなければいけませんから、それまでにその手前までの
$1 + 2 + 3 + 4 + 5 + 6 = 21$進む
よって、$21 \div 7 = 3$(周)$\cdots 0$
つまり、最後の「$7$」に到達する前にもとの「$1$」の位置へ戻ってきてしまいますね。
算数で必要となる思考力を培うためのポイント
算数で必要となる“思考力”とは先ほども記しましたように、
といったものです。
この力を培っていくためのポイントを以下に記したいと思います。
- 試行する際に漠然と解き始めるのではなく、「問題文・例」を最大限活用する
- (図形問題等では)何を求めたいかの“方針・目標”を明確にする
- 試行しながら検証する
- 出題者の意図、理屈・ルールを理解する
- 持っている“知識”を利用する
- ①を利用しながら「一般化・抽象化」してみる
- “他者”へ説明する(アウトプット)
こういったことを学習する際に頭において取り組んでみてくださいね。