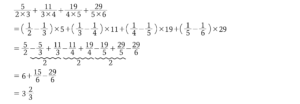前回(第15回)まで様々な単元における“技術”“着眼点”に関して記してきました。
意識は全くしておりませんでしたが、そこまでの15回を第1部とし、今回からは“第2部”と称して最近の入試問題を題材に、さらに算数の“深み”へ入っていきたいと考えています。今後ともどうぞお付き合いください。
身につけておきたい「計算の工夫」
さて、その第2部の第1回として「計算の工夫」を取り上げます。
中堅校から難関校までたくさんの学校の入試問題で、大問1を中心に計算問題が出題されます。今年度(2024年度)も様々な学校で「計算問題」が出題されました。いくつかのパターンがありますが、共通していえることは“やり方さえ知っていれば誰にでもできる”ということです。
出題する側は「腕力」だけを求めているのか
しかしながら“腕力”だけでこなすと大変そうで、時間がかかってしまう問題も多く見られます。はたして出題する学校側は“腕力”だけを求めているのでしょうか?
以下の入試問題を例にとって見てみましょう。
①の解説:分配法則の逆を利用する
$5.3 \times 1.25 + 96 \times 0.125 + 125 \times 0.152 + 0.83 \times 12.5\\
=53 \times 0.125 + 96 \times 0.125 + 152 \times 0.125 + 83 \times 0.125\\
=(53 + 96 + 152 + 83) \times 0.125\\
=(53 + 96 + 152 + 83) \times \frac{1}{8}\\
=384 \times \frac{1}{8}\\
=\underline{48}$
“分配法則の逆”を利用するために、“$\times 0.125$”にそろえるといった計算の工夫をしていますね。また“$0.125=\frac{1}{8}$ ”は多くの受験生が知っているであろう計算の知識も利用していますね。
②の解説:部分分数分解(キセル算)
こちらも中学入試の計算問題としてはお馴染みの“部分分数分解”といったものですが(“キセル算”なんていう呼び名もありますね)、こちらも工夫と知識の利用が必要です。
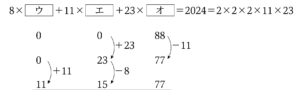
③の解説:不定方程式(イモヅル算)
“不定方程式”といったものですが(“イモヅル算”なんていう呼び名もありますね)、様々なアプローチがある計算です。
ここでは一般的なアプローチではありませんが、この年度(2024年度)に受験する受験生たちの多くが“$2024 = 2 \times 2 \times 2 \times 11 \times 23$”という“素因数分解”の知識を知っていたであろうことを利用して、“直感的”にイモヅル式に解答してみました。入試問題としても遊び心がありますね。
どんな受験生にも必須の「計算問題」
中堅校であればあるほど計算の出題頻度は増していきます。たとえ計算問題の出題がない学校でも、大問を解く中でほぼ全ての問題で“計算処理”が必要となります。つまりそれだけ計算問題はどんな受験生にも必須です。
計算を道具として使いこなせるか、頭を使ってきたかを確認する
ところでなぜこのような計算問題を出題するのでしょうか?
出題者側としては、中学校で学ぶ「数学」につなげるため計算を道具として使いこなせているかどうかを見たいのだと思います。さらに計算問題の練習をする中で頭を使ってきたかを見たいのでしょう。
限りがある試験時間の中で“処理上手”となり、“ミスを減らす”ようにするためにも、日々の“計算トレーニング”はとても大切です。漫然と計算をするのではなく、“工夫”を意識してください。そうすれば計算が“頭を鍛える”トレーニングにもなりますよ。