「剰余」の考え方【中学受験生が身につけておきたい「計算の工夫」③】

これまで第２部に入ってから「数（計算）」を扱ってきましたが、今回はそういった数を考える中でもやはり重要な“剰余（余り）”に注目してみたいと思います。

教科別コラム

素因数分解の利用【中学受験生が身につけておきたい「計算の工夫」②】

中学受験指導スタジオキャンパス算数科の内田実人先生が、最近の入試問題を題材に、算数の“深み”に迫っていく連載。今回は「素因数分解」を活用した計算の工夫についてご紹介します。...

中学入試の頻出テーマ「余りの和や積」「余りの周期」

その中でも“余りの和や積”“余りの周期”といったテーマは現在の中学入試においても頻出となってきています。理由については後述することにして、さっそく出題例を見てみましょう。

取り上げた灘中の問題を解いてみましょう。

さすがに$2$を$2022$個かけた数$(=2^{2022})$は計算するのは厳しいですね。

「余りの和や積」「余りの周期」に注目した工夫

さて皆さん、①は確かに上記のように直接計算しても求められますが、②を求めるためにはどうしたらよいのでしょうか？
そこで今回のテーマ“余りの和や積”“余りの周期”に注目してみましょう！
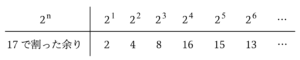
$2$を$n$回かけた数とその数を$17$で割った余りを表にしてみます。

このとき、
$2^1 (=2)$を$17$で割った余りは$2$
$2^2 (=4)$を$17$で割った余りは$4$
$2^3 (=8)$を$17$で割った余りは$8$
$2^4 (=16)$を$17$で割った余りは$16$

というように割られる数が$2$倍になれば余りも$2$倍になっていますよね。

ところが$2^5 (=32)$は表にあるように余りは$15$となってしまっています。確かに$2^5 (=32)$を$17$で割った余りは$15$です。ここでは“余りも$2$倍”となる規則は崩れてしまったのでしょうか？

そうではありません。$17$で割った余りが$32$となれば、もう一回$17$で割れますから
$32 \div 17 = 1 \dots 15$　となり、余りは$15$となります。

それではその次の$2^6 (=64)$を$17$で割った余りは、この$15$を$2$倍した数となっているでしょうか？
$15 \times 2 = 30$ですが、この$30$をもう一回$17$で割って
$30 \div 17 = 1 \dots 13$　確かに余りは$13$です。

なるほど、やはり余りは$2$倍（$17$より大きくなればもう一回$17$で割る）となっていますね。
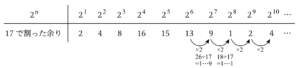
表を続けてみましょう。

①の答え$4$

「余りの周期」を用いて②を解く

さあ、続けて②です。皆さん、上の表を見て何か気づきましたか？

そうです。$17$で割った余りは“$2, 4, 8, 16, 15, 13, 9, 1$”という$8$個ずつの周期となっていますね。
よって、$2$を$2022$個かけた数$(=2^{2022})$を$17$で割った余りは、

$2022 \div 8 = 252$（周期）$\dots 6$（個）

より、周期の$6$番目の$13$ですね。

②の答え$13$

高レベルの学校で今後も取り上げられるであろう「余りの和や積」「余りの周期」

こういった“余り”に関する問題は、レベルにかかわらず幅広く中学入試において出題されます。さらに今回のような“余りの和や積”“余りの周期”といったテーマとなってくると、より高いレベルの学校において取り上げられるようになります。

特に “灘”での出題はその後の中学入試問題における最大の参考材料となっており（数年前の“灘”中入試問題がどこかの学校でも出題されるなんてことが、今や当たり前となっていますね。そういう意味では今の中学受験生は大変です！）、今後幅広く出題されていくことでしょう。

大学入試での出題が中学入試に影響を及ぼす？

それではなぜ“灘”を中心とした上位難関校とよばれる学校が、このようなテーマの問題を出題するのでしょうか？

そうです。“東大”をはじめとする大学入試での出題が大きく影響しています。今回のテーマとなる“余りの和や積”“余りの周期”といった問題も、毎年のように“東大”入試で出題されています（高校数学では「合同式」とよばれますね）。

ちなみに同じ年度の“東大”入試では以下のような出題がありました。

こういった数学の世界においては“抽象的”に求めていくような事柄を、“具体的”に試行錯誤させつつ考えていくことが算数といえるでしょう。

もちろん興味がある人は、知識として吸収することは大変素晴らしいと思います。しかしやはり普段からの取り組みにおいて試行錯誤した上での規則などの検証といった行動が、より高いレベルの問題に太刀打ちできる基本となると思います。その上で知識としてしまえば“鬼に金棒”ですね。

最新年度の市川中の出題例を確認！

最後にもう一つ今年度からの出題例です。

解説

よって、$75$個$+ 225$個$= 300$（個）