
前回まで、ある単元にスポットライトを浴びせ、その単元においてトピックスとなる問題を取り上げてきました。今回は少し趣きをかえ、「会話文」形式の問題を取り上げてみました。
実はこのような「会話文」形式の問題は以前より公立中高一貫校の“適性検査問題”においては、普通に出題されてきました(ほとんど全ての問題が数人の会話で構成されています)。ところが最近の入試問題を見ていると、様々な私立の学校でこの「会話文」形式での出題があります。
大学入試における変化が中学入試に与える影響
一体その広がりの理由は何なのでしょうか?
そうです。大学入試における変化です。2021年度から始まった「大学入学共通テスト」の問題を見てみましょう。
花子さんと太郎さんは、次の二つの2次方程式について考えている。$x^2 + px + q = 0$……①
$x^2 + qx + p = 0$……②
①または②を満たす実数$x$の個数を$n$とおく。(1)$p = 4$、$q = -4$のとき、$n =$ ア である。
また、$p = 1$、$q = -2$のとき、$n =$ イ である。(2)$p = -6$のとき、$n = 3$になる場合を考える。
| 花子:例えば、①と②をともに満たす実数$x$があるときは$n = 3$になりそうだね。
太郎:それをaとしたら、$a^2 - 6a + q = 0$と$a^2 + qa -6 = 0$が成り立つよ。 花子:なるほど。それならば、$a^2$を消去すれば、$a$の値が求められそうだね。 太郎:確かに$a$の値が求まるけど、実際に$n = 3$となっているかどうかの確認が必要だね。 花子:これ以外にも$n = 3$となる場合がありそうだね。 |
$n = 3$となる$q$の値は
$q =$ ウ 、 エ
である。ただし、 ウ < エ とする。
大学入学共通テスト「問題作成方針」で挙げられた3つの方針
大学入試センターが発表した共通テストの「問題作成方針」には、以下の3点が挙げられています。
- 大学入試センター試験及び共通テストにおける問題評価・改善の蓄積を生かしつつ、共通テストで問いたい力を明確にした問題作成
- 高等学校教育の成果として身に付けた、大学教育の基礎力となる知識・技能や思考力・判断力・表現力を問う問題作成
- 「どのように学ぶか」を踏まえた問題の場面設定
特に3つ目の、授業において生徒が学習する場面や、社会生活や日常生活の中から課題を発見し解決方法を構想する場面など、学習の過程を意識した問題の場面設定を重視することから「会話文」形式を用いることで、全体的に“読ませる”“考えさせる”設定になっています。
中学入試でもさまざまな学校で「会話文」形式の出題が見られる
こういった流れが中学入試においても取り入れられることで、様々な学校で「会話文」形式の出題があるのですね。(「会話文」形式ではありませんでしたが、とうとう開成においても開成(あけなり)君が登場したのはこの流れからなのでしょうか?(笑)
形式はみな「会話文」とはいえ、取り上げられた題材やレベルは学校によってまちまちです。ざっと挙げてみても、“覆面算・魔方陣・操作計算(コラッツ予想)・数独・約数・倍数・N進法・一筆書き・場合の数(漸化式)・ゲームの必勝法・平面図形(合同)・立体図形(正多面体)・三角数・四角数”etc.と様々です。
2022年度市川中で出題された「覆面算」
今回は以下、2022年度の市川中の問題を取り上げてみました。年齢問わず取り組める(他校でも同じ題材からの出題がありました)“覆面算”です。
それでは見てみましょう。
以下の会話文中の ア から ク にあてはまる数を答えなさい。ただし、答えが複数ある場合はすべて答えなさい。
X:「下の筆算が成り立つように、各アルファベットに$0$から$9$までの数を$1$つずつ入れることを考えよう。」
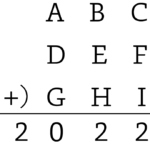
Y:「それなら簡単だよ。$\rm{A}$と$\rm{D}$と$\rm{G}$が$6$で、$\rm{B}$と$\rm{E}$と$\rm{H}$が$7$で、$\rm{C}$と$\rm{F}$と$\rm{I}$が$4$ならば、$674 + 674 + 674 = 2022$が成り立つよ。」
X:「そうだね。では、同じ数が使えなかったらどうだろう。各アルファベットに入る数が異なるように、$0$から$9$までの数を$1$つずつ入れられるかな。まず、一の位の数のみに着目すると、$\rm{C} + \rm{F} + \rm{I}$として考えられる値は何があるだろうか。」
Y:「 ア が考えられるね。」
X:「次に、繰り上がりと十の位の数のみに着目して$\rm{B} + \rm{E} + \rm{H}$の値を考えてみよう。」
Y:「 イ が考えられるね。同じようにして$\rm{A} + \rm{D} + \rm{G}$の値は ウ が考えられるよ。」
X:「これだけだと、まだ各位の数の和の候補が多くて決められないね。でも、各アルファベットには$0$から$9$までの中から異なる$9$つの数が入ることを考えると、各位の数の和の組合せは$1$通りに絞られるんじゃないかな。」
Y:「$\rm{C} + \rm{F} + \rm{I} =$ エ 、$\rm{B} + \rm{E} + \rm{H} =$ オ 、$\rm{A} + \rm{D} + \rm{G} =$ カ だね。ということは、$0$から$9$の中で使わない数は キ なんだね。」
X:「では、$\rm{A}$が$7$のとき、残りのアルファベットに入る数の組合せが何通りあるか求めてごらん。」
Y:「わかった。 ク 通りだね。」
解説
ア
最小 $0 + 1 + 2 = 3$ 以上
最大 $7 + 8 + 9 =24$以下 で一の位が$2$なので、$12$か$22$
イ
ア $ = 12$のとき、 $1 + \rm{B} + \rm{E} + \rm{H} = 12$か$22$
⇒$\rm{B} + \rm{E} + \rm{H} = 11$か$21$
ア $ = 22$のとき、 $2 + \rm{B} + \rm{E} + \rm{H} = 12$か$22$
⇒$\rm{B} + \rm{E} + \rm{H} = 10$か$20$
ウ
イ $ = 10$か$11$のとき、 $1 + \rm{A} + \rm{D} + \rm{G} = 20$
⇒$\rm{A} + \rm{D} + \rm{G} = 19$
イ $ = 20$か$21$のとき、 $2 + \rm{A} + \rm{D} + \rm{G} = 20$
⇒$\rm{A} + \rm{D} + \rm{G} = 18$
エ , オ , カ
$\rm{A}~\rm{I}$ $9$つの和
最小 $0$~$8 = 36$以上
最大 $1$~$9 = 45$以下
$\rm{C} + \rm{F} + \rm{I} = 22$とすると、$\rm{B} + \rm{E} +\rm{H}$, $\rm{A} + \rm{D} + \rm{G}$ともに最小の$10$, $18$としても$9$つの和は
$22 + 10 + 18 = 50$となってしまうので×
よって、$\rm{C} + \rm{F} + \rm{I} = 12$… エ
⇒$\rm{B} + \rm{E} + \rm{H} = 11$か$21$
$\rm{B} + \rm{E} + \rm{H} = 21$とすると、$\rm{A} + \rm{D} + \rm{G}$を最小の$18$としても$9$つの和は
$12 + 21 + 18 = 51$となってしまうので×
よって、$\rm{B} + \rm{E} + \rm{H} = 11$… オ
すると、$\rm{A} + \rm{D} + \rm{G}=19$… カ
キ
$45 - (12 + 11 + 19) = 3$
ク
$\rm{A} + \rm{D} + \rm{G} =19$ $\rm{A} = 7$より、$\rm{D} + \rm{G} = 12 = 4 + 8$($3$と$7$は使えないので)
$\rm{D} + \rm{G} = 12 = 4 + 8$
⇒$\rm{C} + \rm{F} + \rm{I} = 12 = 1 + 2 + 9$
⇒$\rm{B} + \rm{E} + \rm{H} = 11 = 0 + 5 + 6$
このときの並べ方は、$(2 \times 1) \times (3 \times 2 \times 1) \times (3 \times 2 \times 1) = 72$(通り)
$\rm{D} + \rm{G} = 12 = 4 + 8$
⇒$\rm{C} + \rm{F} + \rm{I} = 12 = 1 + 5 + 6$
⇒$\rm{B} + \rm{E} + \rm{H} = 11 = 0 + 2 + 9$
このときも並べ方は$72$通り
よって、$72 \times 2 = 144$(通り)



















