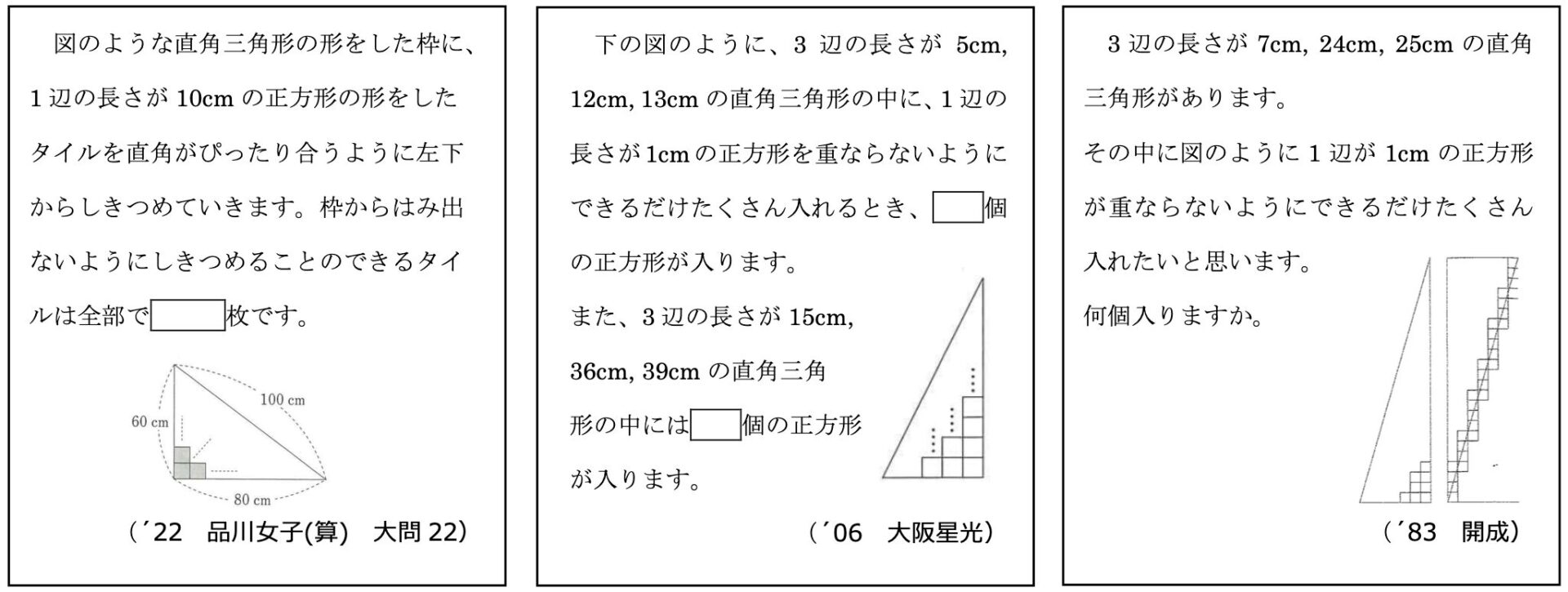
右のマス目に、1から8までのすべての整数をあてはめた表を作ります。左隣の数より大きく、真下の数より小さくなるようにあてはめた表は全部で何通りできますか。
(´22 青稜2-B 大問4)
右の枠に1から8までの数をひとつずつ入れます。どの数も、右隣りの数より小さく、また真下の数より小さくなるように入れるとき、何通りの並べ方がありますか
(´08 慶應普通部 大問7)

右のマス目の中に1から8までの数字8個を、横のならびはどちらも右に行くほど大きくなり、たてのならびはすべて下の方が上よりも大きくなるように入れて行く方法は全部で 通りある
(´90 灘(1日目) 大問10)

歴史は繰り返す――過去に出題された問題がほとんどそのまま蘇る理由
今回も少し趣向を変えて“歴史はくり返す”をテーマに入試問題を見ていきたいと思います。上記3題をご覧になってどういった感想を抱かれたでしょうか?
“35年前くらいの灘中と同じ問題だ!”
“何回も同じ問題が出題されてる!”
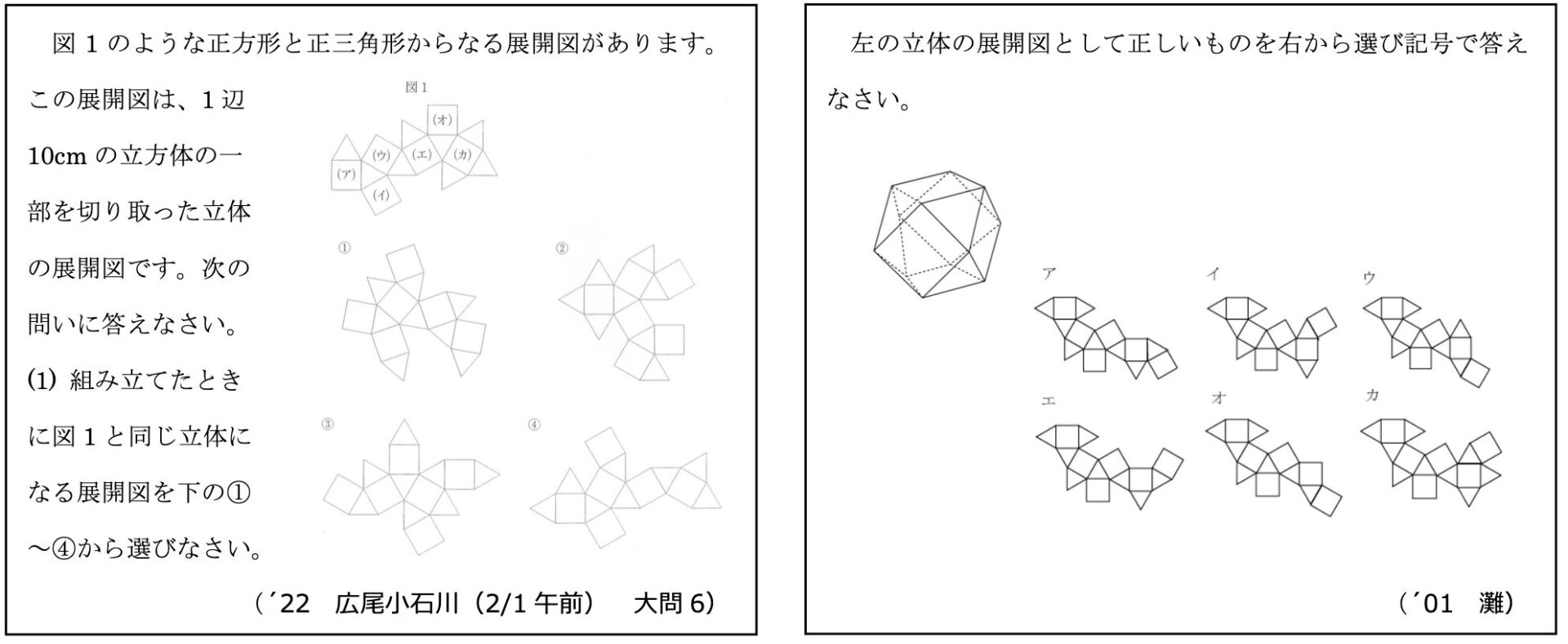
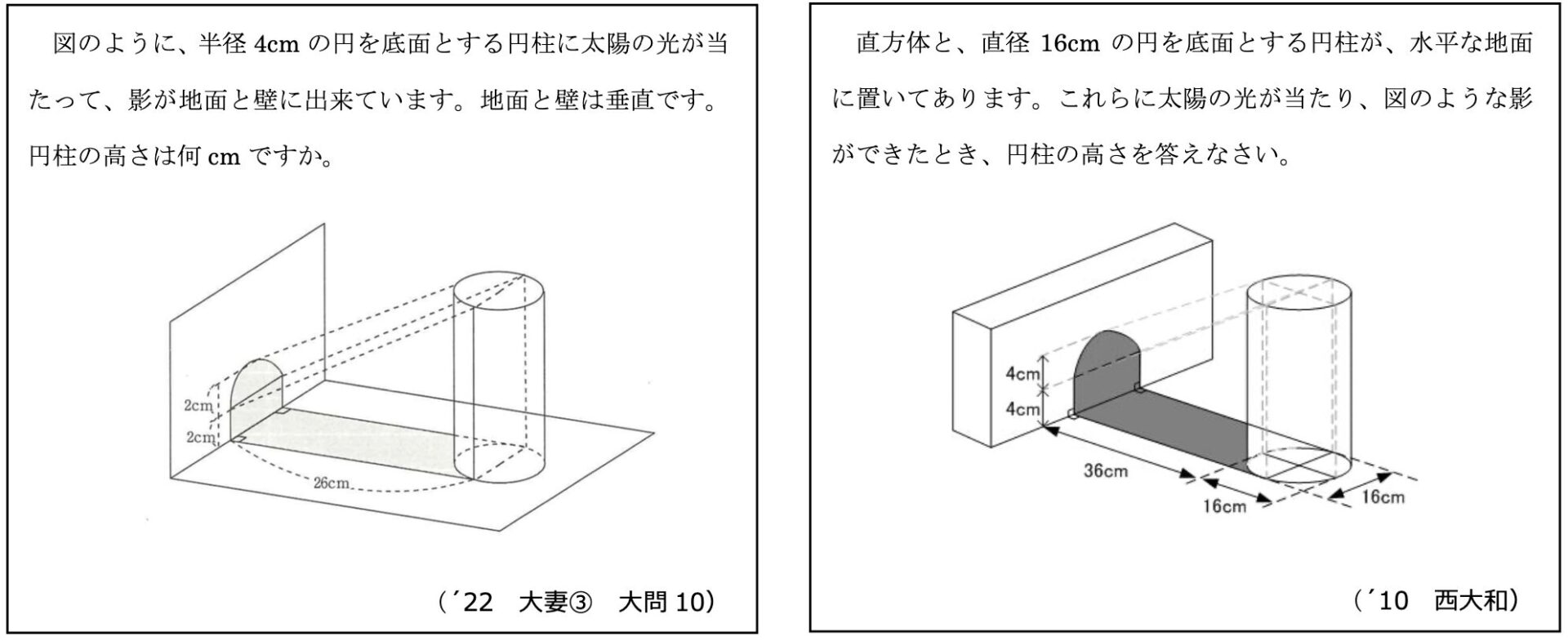
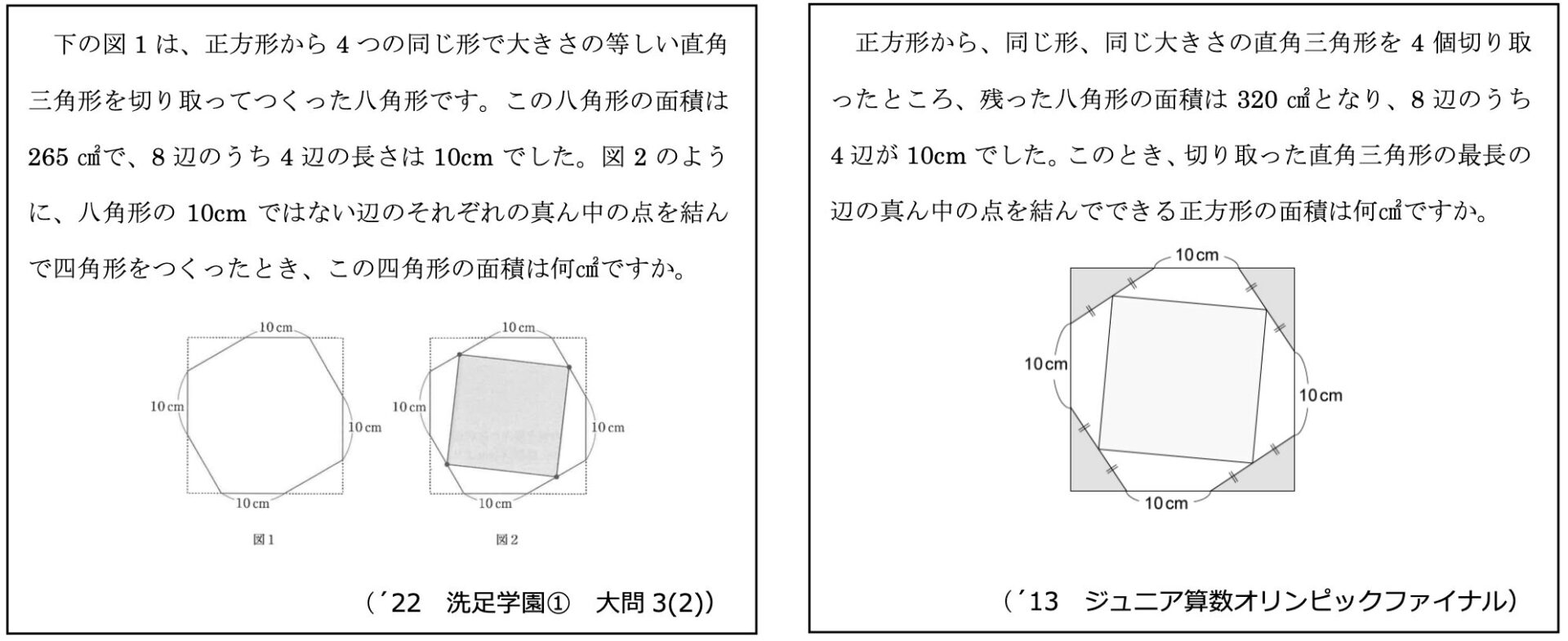
こんな感想を抱かれたのではないでしょうか。確かに過去出題された問題が、ほとんどそのままの形で蘇ることは上記の例だけではありません。以下の例も見てみましょう。
今回取り上げた問題のみならず、様々な単元で最難関とよばれる学校の入試問題が蘇っていることがおわかりになると思います。しかもほぼそのままの形で蘇っている問題、何度も出題されている問題もありますね。(例4)は算数の強者が集結する「ジュニア算数オリンピック決勝戦」の問題が蘇っていますね。
受験生の「力」を図れる問題だから出題される
学校側は過去に最難関中で出題されている問題を真似して出題しているだけなのでしょうか?
そうではありません。過去に出題されている問題を見てみると、いずれも今や塾のテキスト・参考書等に載っているような良問といっていいでしょう。つまり、それだけ受験生の「力」をはかれる問題なのです。
過去に出題された「良問」に現在の中学受験生が対処する方法
とはいえ現在の中学受験生は大変です。かつての(今の中学受験生の保護者世代)に比べて圧倒的に学習領域が広がっており、さらには前回・前々回でもご紹介したような、“会話文”“説明”“複数解答”“長文”といった形式に対する準備も必要となっています。
基本事項を理屈とともに吸収し、他者を意識したアウトプットする訓練を積む
これからの中学受験生は、今まで以上に塾のテキストにあるような例題等の基本事項を、テクニックのみならず、しっかり“理屈”とともに吸収することが大切となります。さらにそれらを他者を意識してアウトプットする訓練も行いたいですね。それにより長い文章問題等であっても、解く際に途中過程を整理していく中で、今までに経験した問題の一種であることが判断されていくこととなります。
冒頭の問題の解説
それでは問題の解説です('22 青稜2-B 大問4)。
何も知識がなく“パズル”的に当てはめようとすると大変そうですね。
もちろん知識・経験があれば「カタラン数」の問題であり、以下の最後の解法で解決してしまいます(今でこそ塾テキスト・参考書にも必ず掲載されていますが、昔の受験生は大変だったことでしょう)。
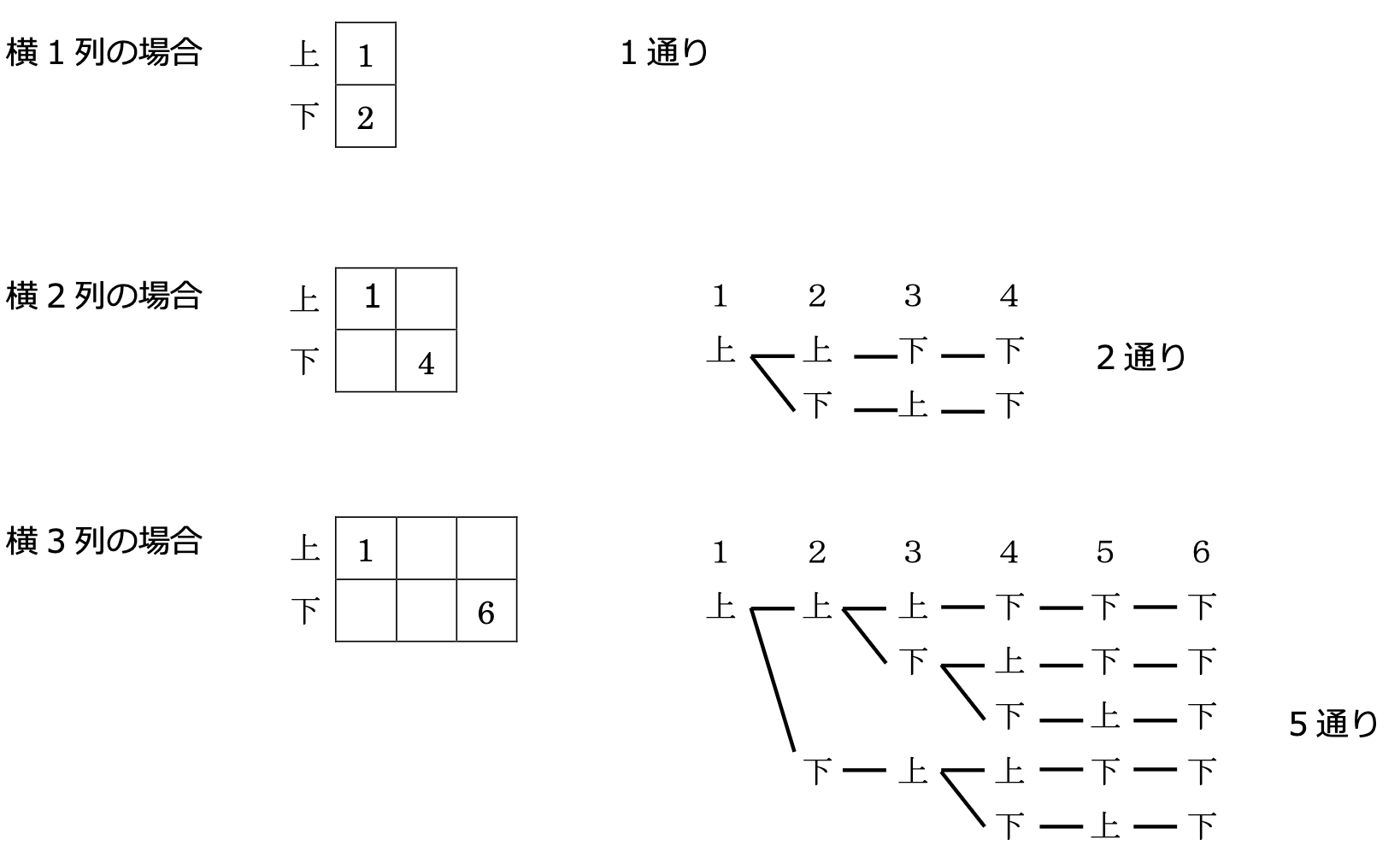
“小さな”場合で試してみる
さて、こういった場合はまずは“小さな”場合で試してみましょう。
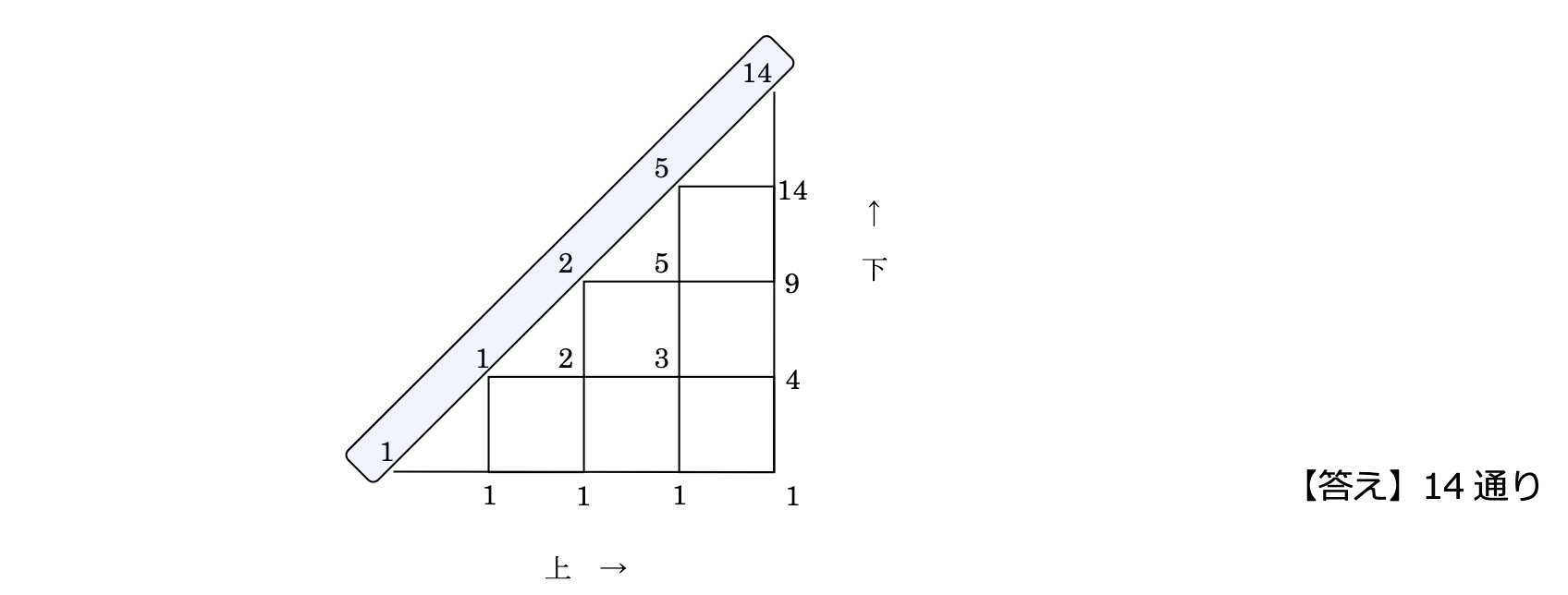
「カタラン数」→“道順解法”を利用する
このまま“横4列”の場合を樹形図を利用して求めることもできます。しかしながら、試験時間を考えると厳しそうですね。
そこで様々な知識や経験をもとにこの樹形図のかき方を検証すると、樹形図の左側から右隣りへかく際に“下が上の個数をこえない”ようになっていることから、「カタラン数」であることが判明します(“ヒツジとオオカミの問題”を経験したことのある方もいらっしゃることでしょう)。すると今や定番になっている以下の“道順解法”が利用できます。