
向きが変わったとたんに…(公式に頼るだけの子)
前回まで「計算力」をテーマにして、中学受験に向けた算数のアドバイスをさせて頂きました。今回からは「平面図形」を取り上げてみたいと思います。まずは過去にあったエピソードから。
先日、普段私が指導させて頂いている「中学受験指導スタジオキャンパス」小学校5年生の授業において、「平面図形」をテーマにした導入で、以下のような問題に取り組んでもらいました。
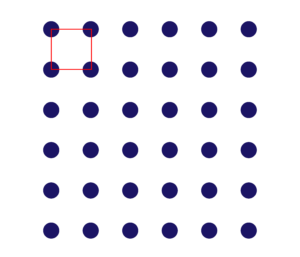
ほとんどのお子様が短時間で2番目の大きさと思われる正方形をかいてくれました。
ところでどんな正方形だったと思われますか?
皆さんも実際に想像してみてください。
ほぼ全員のお子様が下のような正方形をかいていました。
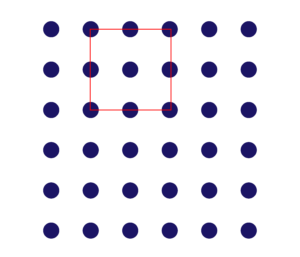
実はこれ、3番目の大きさの正方形なんですよね(大きさは「4」です)。
2番目の大きさの正方形は以下の通りです(大きさは「2」ですね)。
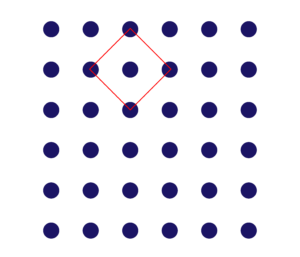
やっぱりか!
もちろん「それは3番目の大きさだよ。もう少し小さい大きさの正方形がかけるんじゃない?」と伝えると、「2」の大きさの正方形をかいてくれるお子様が増えますが、それでも以下のような
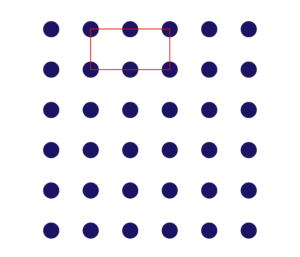
「たしかに大きさは『2』だけど、それって長方形だよ。」というお子様も見受けられました。
「なかなか根深いぞ!」と思いながら、「傾いたり、回転したりしても正方形は正方形だよね。」と言いながら、「じゃあ続けて4番目をかいてみよう!」と伝えると、多くのお子様が
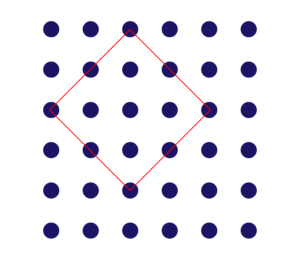
と、5番目の大きさの正方形をかいちゃいました(大きさは「8」ですね)。
ちなみに4番目の大きさは以下のような傾きの正方形ですね。
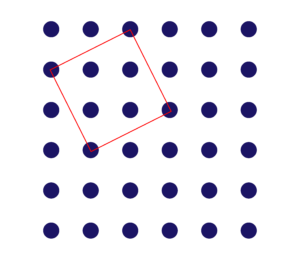
試行錯誤してくれて、こういう時間はとても大切だと思いながらも、次の一手を打てない(経験がない、知識がない)お子様が多いなあとも正直感じました。また、習ったこと, 「公式」等で覚えたことが全てであるという認識のお子様も多いのかなとも感じました。この4番目の大きさの正方形は、以下のように「分ける(分割する)」ことによって大きさは「5」であることがわかりますね。
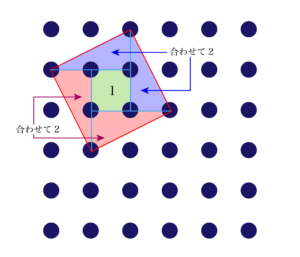
三角形の面積
また、別の授業において「三角形の面積」の復習をする場面がありました。その際提示した問題が以下のような三角形の面積を求める問題でした。
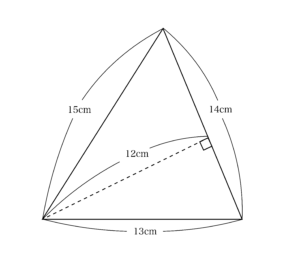
もちろん「直角」の記号もあることから、多くのお子様が正解しました。しかしながら、それでも何名かのお子様は「13×14÷2」のように、公式は覚えているものの「底辺」や「高さ」の意味がきちんと捉えられておらずに、習った「見た目」だけで公式に数を当てはめてしまって間違っていました(中には右下の角に「直角」記号を無理やりかいている子も…)。
手を動かす・図をかく
これらのエピソードから、たくさんのお子様方が学習する上で「手を動かす」「図をかく」「理屈を理解する」といったことを避けて、「公式に当てはめる」「見た目で解く」「(悪い)直感に頼る」といったことがクセづけられてしまったことを感じざるをえません。
以下、「折り紙」を使った例や「図」をかく意味の例です。
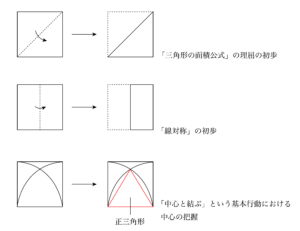
「平面図形」における初回として、今回はエピソードを交えて記しました。次回からは、実際の図形問題に対する取り組みを具体例を示しながらお伝えできればと考えています。お楽しみに。



















