5年生で計算単元を扱うことが増えてきました。
それとともに「うちの子は計算が苦手で……」といったご相談をよく受けるようになります。
理科の計算の基本は「比例」と「反比例」
計算問題(特に力学や化学計算)を苦手にする生徒の多くは、解く上での必要な手順がいい加減になっている傾向にあります。
手順を守らず、メモ書きもない……そして解けない、となれば要注意。声をかける必要がありそうです。
「ばね」の問題から学ぶ「メモの仕方」
今回は「ばね」の問題を例に挙げて、メモの仕方(私は「ならべ算」と呼んでいます)をご紹介しましょう。
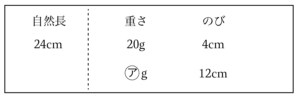
ばねについては「3つの長さ」を整理するところから始めます。
そして、以下の法則が重要です(フックの法則)。
例題を通して確認する(1)

これを踏まえて次の問題に取り組んでみましょう。
問題1の解説
全長が$36\rm{cm}$ですので、ばねののびは$12\rm{cm}(36-24)$です。
これを以下のようにメモ書きした「ばね情報」に追記しましょう。
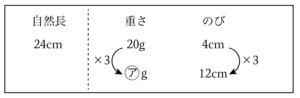
ばねののびが基準の$3$倍になっているので、おもりの重さも$3$倍になっているはずです。
よって、
$㋐=20×3=\underline{60\rm{g}}$
例題を通して確認する(2)

問題2の解説
$30\rm{g}$のおもりをつるすと全長が$37\rm{cm}$
$80\rm{g}$のおもりをつるすと全長が$47\rm{cm}$
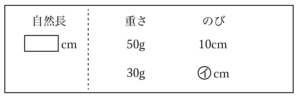
このことから、$50\rm{g}$増えると$10\rm{cm}(47-37)$のびることが分かります。
今回は自然長を問われています。
$30\rm{g}$のおもりをつるしたときのばねののびを求めましょう。
以下のように追記します。
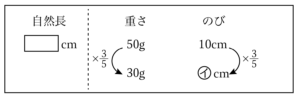
おもりの重さが基準の$\dfrac{3}{5}$倍になっているので、ばねののびも$\dfrac{3}{5}$倍になっているはずです。
よって、
$㋑=10×\dfrac{3}{5}=6\rm{cm}$
$30\rm{g}$のおもりをつるしたとき、ばねの全長は$37\rm{cm}$$(=$自然長$+$ばねののび$)$です。
このとき、ばねは$6\rm{cm}$のびていると手順3で分かったので、
自然長$(\boxed{\phantom{satoh}})=37-6=\underline{31\rm{cm}}$
※「手順2」で$80\rm{g}$のおもりをつるしたときのばねののびを求めても可です。
理科の計算問題克服の鍵は「関係をメモして倍率計算をする」こと
もちろん別解もありますが、代表的なものをご紹介しました。
ぜひ、「基準をメモ」して「倍率計算」をする習慣をつけましょう。基本的に難しい問題でも同じ作業で解くことができるはずです。
次回は中和反応の計算を例に、もう少し説明をしたいと思います。