やみくもに「問題演習」する子
近年中学入試における「科目」も様変わりしてきました。
多くの中学受験生がこの４教科の学習を行っていることでしょう。
「算数」だけが異質なスタートを切っている
さて皆さん、その４教科の学習のスタート地点を思い出してほしいと思います（自分自身でもお子様でもお友達でもかまいません）。
それぞれの科目において、どうも「算数」だけがその他の科目と異質なスタートを切っていなかったでしょうか？
そんなスタートを切っているお子様方を見ていると、算数だけ学習内容の中に「苦痛」しか存在していないように感じられることも多々ありますね。
「出たとこ勝負」にならない、本当の意味で強い人になる
また、前回記事にしたような「手を動かす」「図をかく」「理屈を理解する」といったことをじっくり行ってこずに、やみくもに「問題演習」量だけが多くなってしまったようで、問題にのぞんだ際「出たとこ勝負」になってしまっているお子様が多いように感じます。
「公式の意味を理解する」「求める考え方を知る」「（補助線等）をかく理由をつかむ」といった学習方法を取り入れて、「出たとこ勝負」にならない本当の意味で強い人になってほしいと思っています。
「公式」の意味を理解する・求める考え方を知る
図形の単元では様々な「公式」が出てきます。
「ひし型」から「公式」との向き合い方を学ぶ
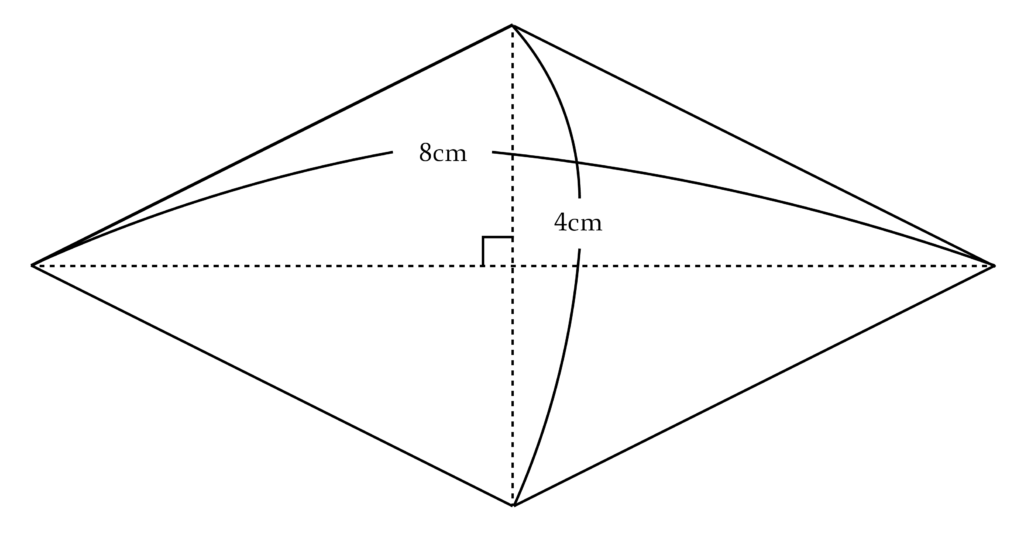
以下のような「ひし形」を例にとって見てみましょう。
この「ひし形」の面積は「対角線$×$対角線$\div 2$」という公式にあてはめて、$4×8\div 2＝16(\rm{cm^2})$と求めることができます。ではなぜ「$\div 2$」なんでしょうか？
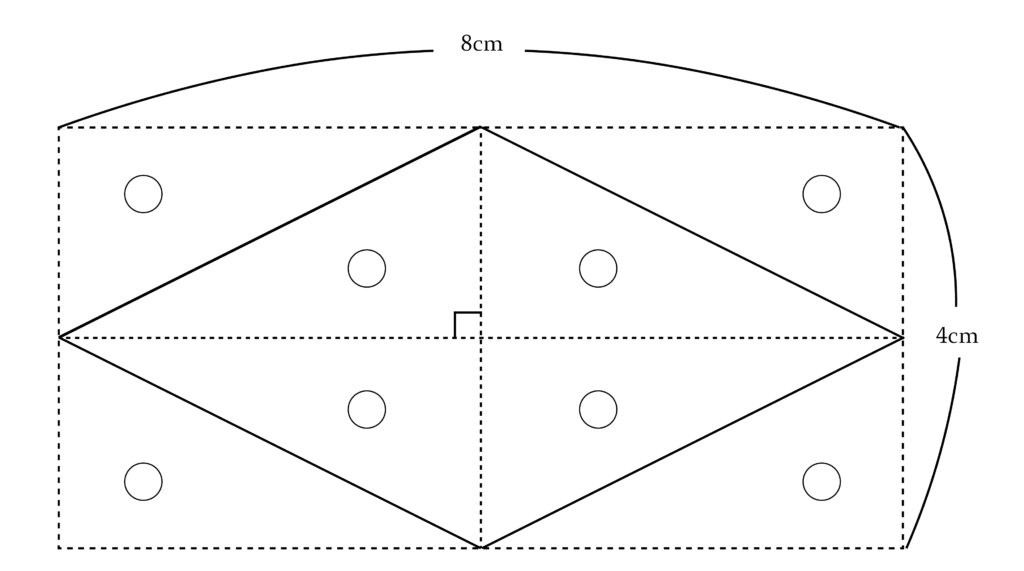
この「$\div 2$」の意味は以下のような図をかくことで理解することができますね。
「公式」の意味を理解することで、形が変わっても対応できるようになる
こういった意味の理解が、少し形が変わった際でもしっかり対応することができます。
以下のような問題においても考え方は変わりませんね。
さらに発展させることができます。
「公式」を覚えるだけにとどまらず、その意味を理解することによって様々応用・発展させることができます。
実はこういった「公式」の意味理解の中には、さらに重要な「求める考え方を知る」といった要素が含まれています。
いずれにしても「図をかく」という「基本行動」をともなっていることは言うまでもありません。
（補助線等を）かく理由をつかむ
やみくもに「問題演習」をしてきてしまったり、「図をかく」ことを怠ってきてしまった場合、特に「補助線」を必要とする問題において、初動となる「基本行動」がともなわず全く求めるものに近づいていないことが多くあります。
例題：「補助線を書く理由」をつかむ学習のイメージ
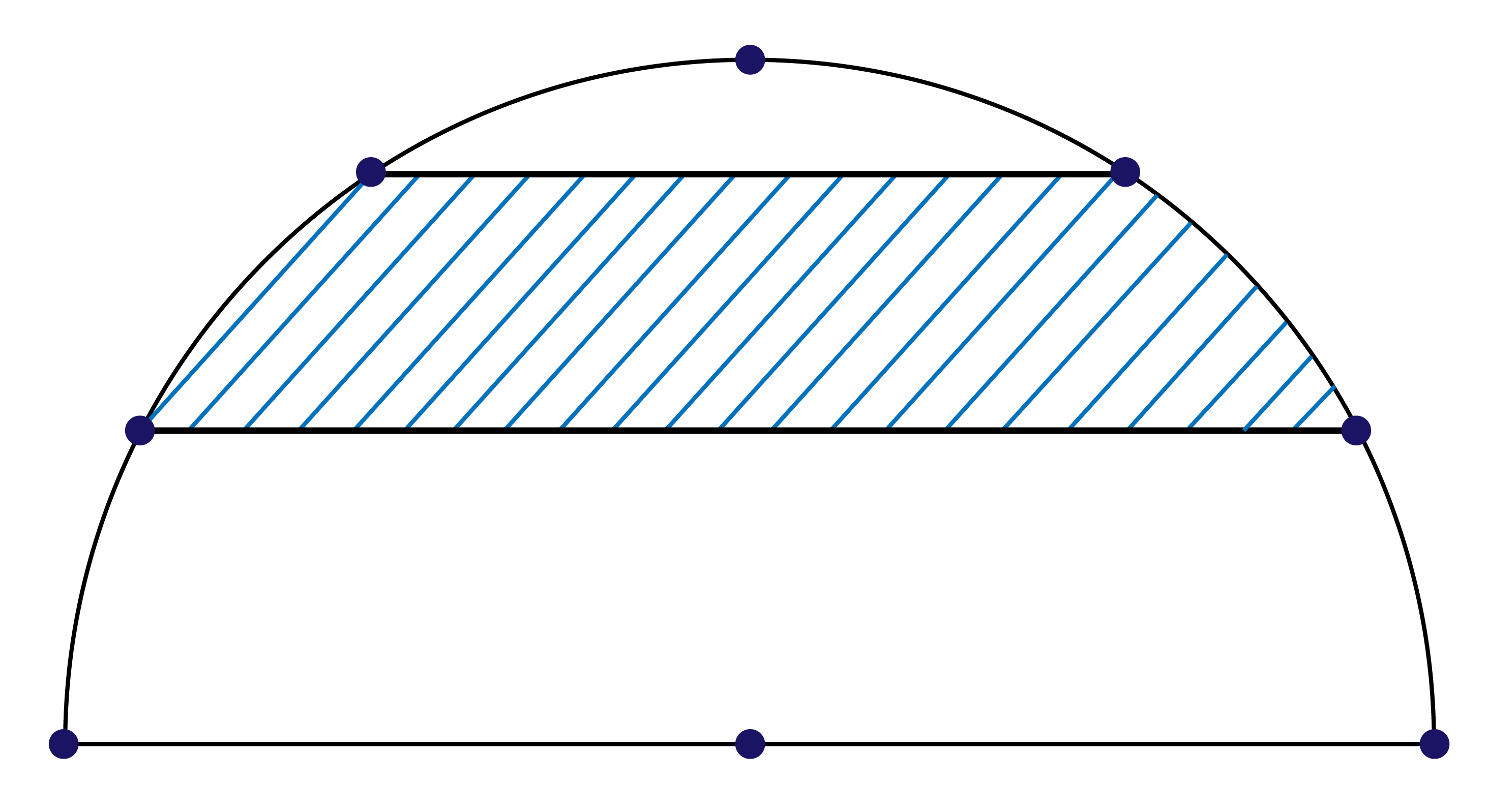
次の問題を見てください。
このとき、斜線の部分の面積を求めなさい（円周率は$3.14$とします）。
当然このままでは求めることはできません。
これが第一段階となります。
どうでしょう。「補助線」を引くことの「基本行動」の型が身についているでしょうか。
さらに、この第一段階がクリアできたとしても、次の段階として引いたことの理由がつかめているでしょうか。
この「補助線」の意味は？
そう「半径」を引いたのですよね。つまり等しい長さの直線を引いたことになります。
ここでもまた段階があります。
そこで今までの「基本の型」が身についているかどうかが問われます。
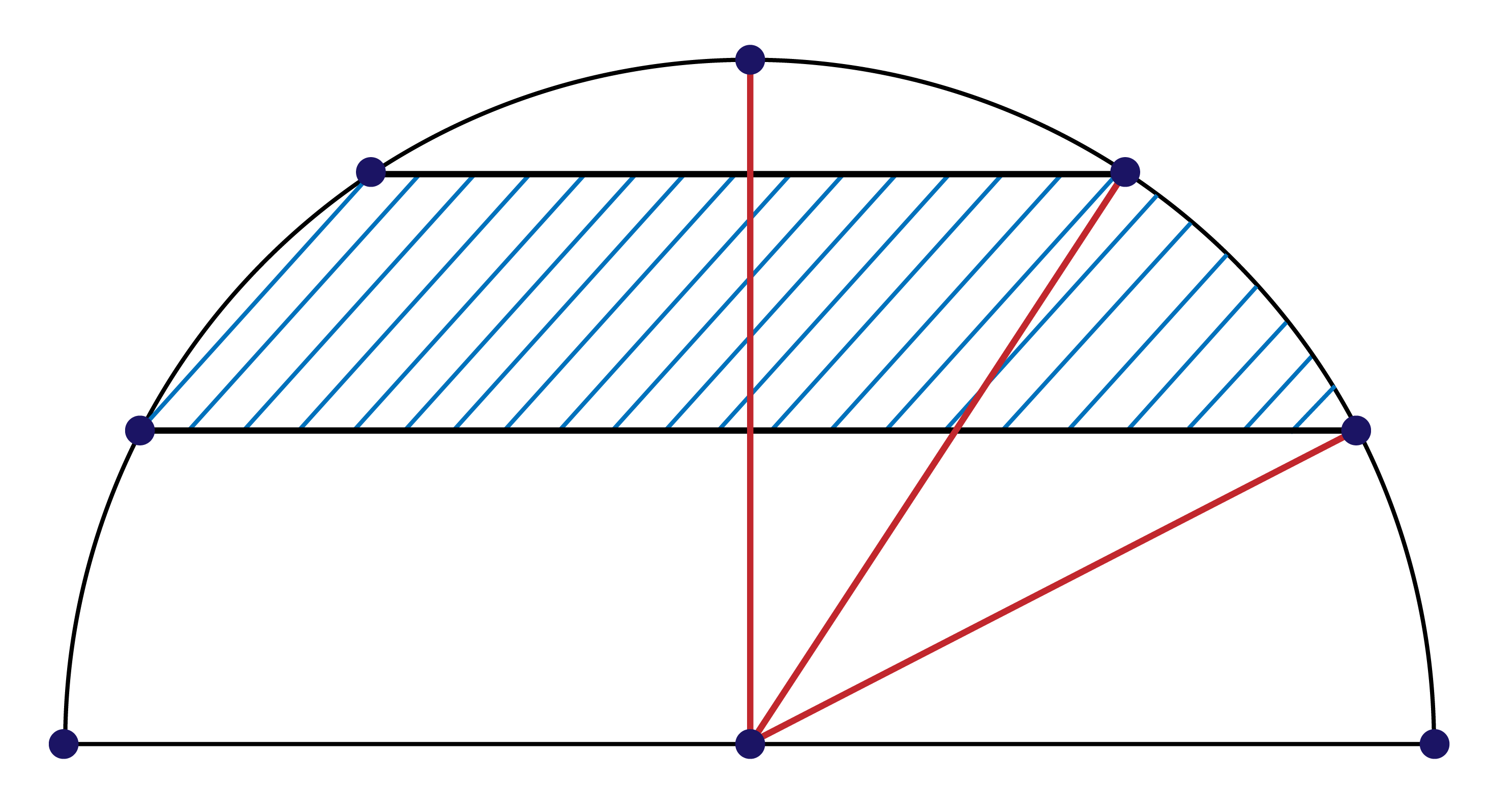
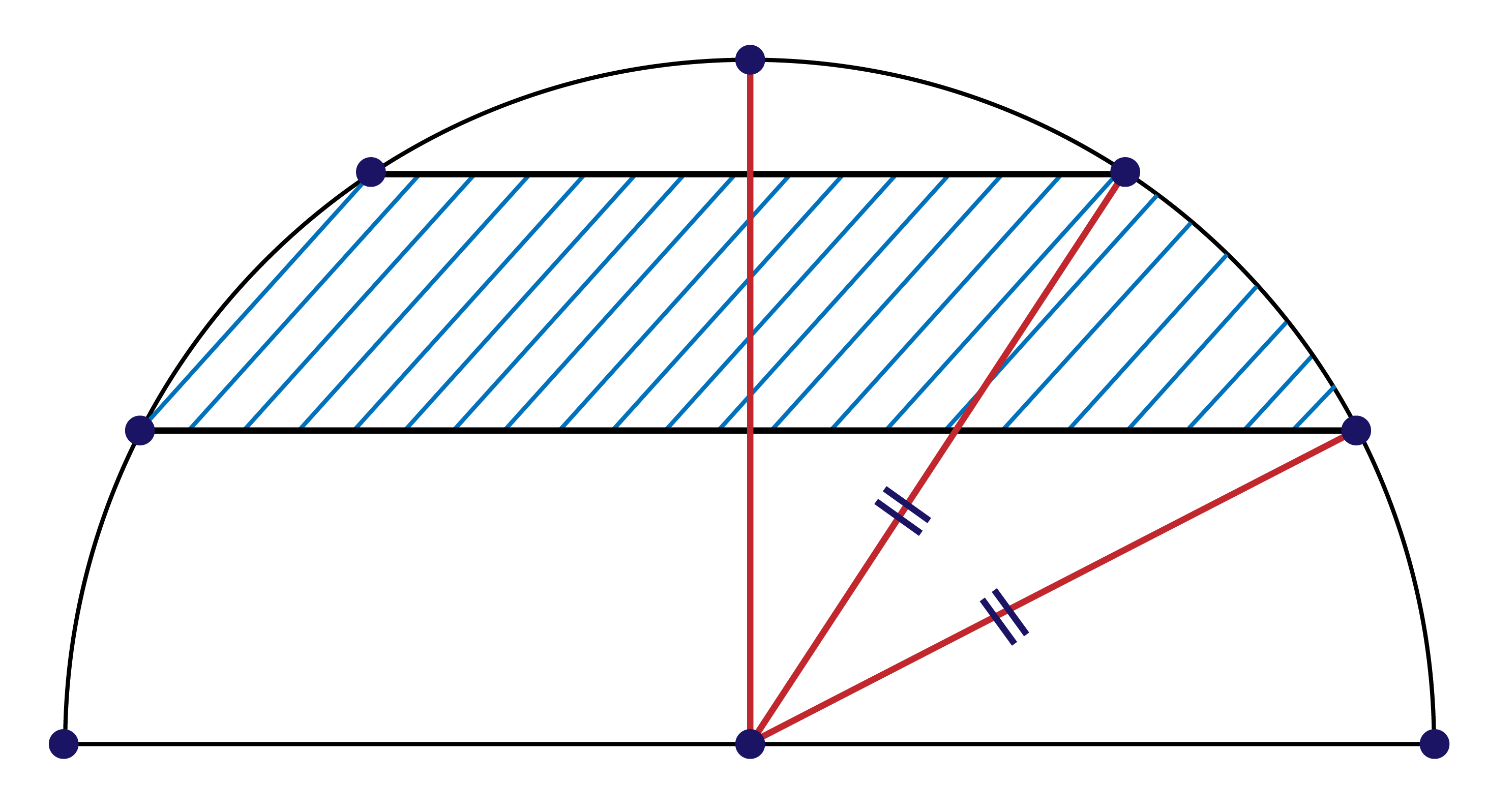
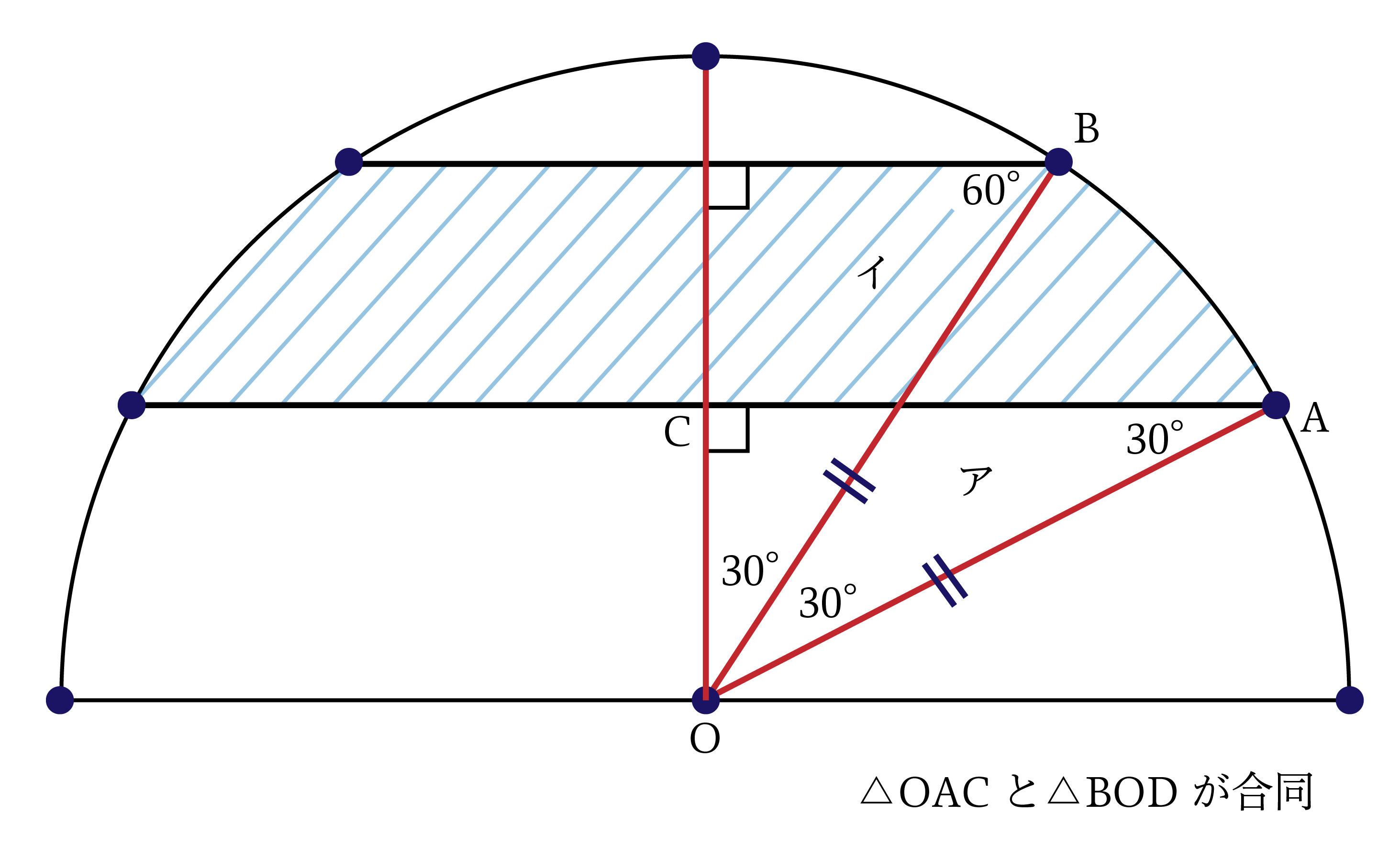
以下のような「合同な三角形を導き出す」ということが「基本の型」の一つなんですよね。
最終的にはアとイの面積が等しいため、イの部分をアの部分へ「等積移動」することで、中心角$30^\circ$のおうぎ形$\rm{OAB}$の$2$つ分として、$12×12×3.14×1/12×2＝75.36（\rm{cm^2}）$と求めることができます。
一つ一つの基本的な「行動」や「理由」を身につけつつ問題に取り組むことで「安定した強い人」になる
このように、一つ一つの基本的な「行動」や「理由」を身につけつつ問題に取り組むことが大切ですね。
やみくもに補助線引けばなんとかなるといった“出たとこ勝負”の演習では、安定した結果を得ることができません。
本当の意味で「安定した」「強い」人になるべく、上記のような取り組みを参考にしてほしいと思います。
